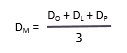Monte Carlo analysis

Die Monte-Carlo-Analyse verwendet eine Drei-Punkte-Schätzung der Dauer für jeden Vorgang in einem Netzplan. Anschließend wird die Methode des kritischen Pfades angewandt, um eine Reihe von Wahrscheinlichkeiten für einen Projektzeitplan zu ermitteln.

 

Die nachstehende Tabelle zeigt die drei Punktschätzungen für sieben Tätigkeiten.

Aufgabe	Optimistisch	Höchstwahrscheinlich	Pessimistisch
A	2	2	8
B	4	5	12
C	7	8	15
D	10	14	18
E	6	7	14
F	7	9	17
G	2	3	10

 

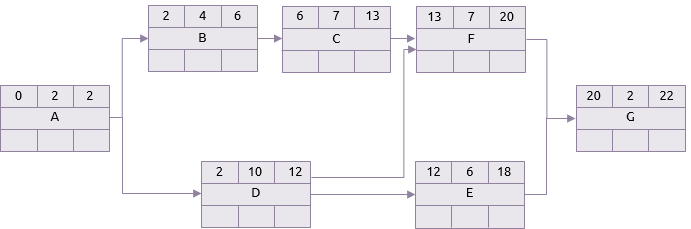
In der Praxis kann jeder der Vorgänge in der obigen Tabelle eine beliebige Dauer zwischen der optimistischen und der pessimistischen Dauer annehmen. Die beiden nachstehenden Netzpläne zeigen den Unterschied zwischen einem Szenario, in dem alle Vorgänge ihre optimistische Dauer einnehmen, und einem Szenario, in dem sie alle ihre pessimistische Dauer einnehmen. Der Übersichtlichkeit halber wird nur der Vorwärtsdurchlauf der Analyse des kritischen Pfades gezeigt.

 

Optimistisches Szenario

 

Pessimistisches Szenario

 

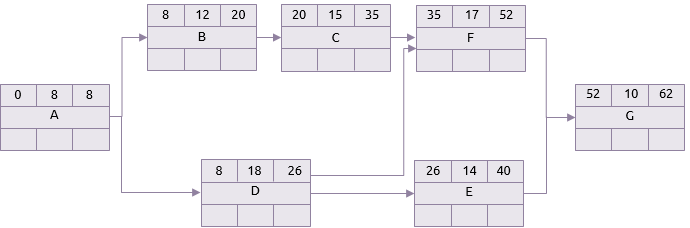
Dieses Projekt könnte also zwischen 22 und 62 Tagen dauern, aber diese beiden Extreme sind die unwahrscheinlichsten Szenarien. Dazwischen gibt es zahlreiche andere. Bei der Monte-Carlo-Analyse wird für jede Aufgabe eine zufällige Dauer aus den angegebenen Bereichen ausgewählt und dann eine Analyse des kritischen Pfades durchgeführt.

Dies kann beliebig oft durchgeführt werden, und Computerprogramme, die dies unterstützen, empfehlen im Allgemeinen, dass 250 - 1.000 Iterationen eine genaue Verteilung der Projektdauer ergeben. Je komplexer das Projekt und je größer die Spanne zwischen optimistischer und pessimistischer Dauer ist, desto mehr Iterationen sind erforderlich.

Wenn man die Häufigkeit jeder möglichen Projektdauer aufzeichnet, ergibt sich in der Regel eine annähernd normale Verteilung.

 

 

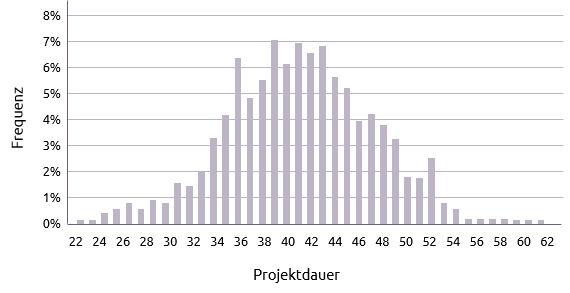
Aus dem obigen Diagramm geht hervor, dass die durchschnittliche Dauer des Projekts etwa 42 Tage beträgt. Das bedeutet, dass eine 50 prozentige Chance besteht, das Projekt bis Tag 42 abzuschließen.

Ein genaueres Bild ergibt sich aus der nachstehend abgebildeten kumulativen Kurve.

 

 

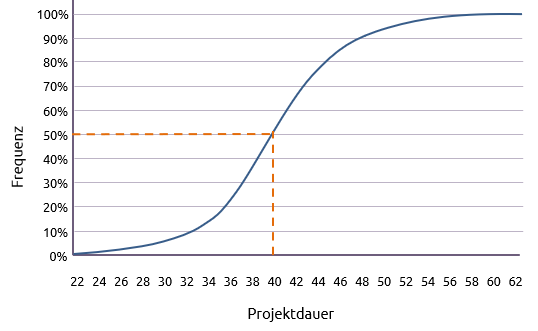
Daraus lassen sich eine Reihe von Fragen beantworten. Zum Beispiel:

"Bis zu welchem Tag besteht eine 50-prozentige Chance, dass wir es schaffen?"

Aus dem Diagramm geht hervor, dass die Antwort Tag 40 ist (auf den Tag genau).

Umgekehrt:

"Wie groß ist die Chance, bis Tag 40 fertig zu werden?"

Die Antwort lautet natürlich: 50%

Nach der Monte-Carlo-Analyse ist es unwahrscheinlich, dass es einen einzigen kritischen Pfad gibt. Daher ist es wichtig, die "Kritikalität" der Aktivitäten zu kennen, d.h. die Häufigkeit, mit der sie auf einem kritischen Pfad erscheinen.

Wenn 1.000 Iterationen durchgeführt wurden, kann es sein, dass es drei mögliche kritische Pfade gibt. Der erste tritt 600 Mal auf, der zweite 250 Mal und der dritte 150 Mal.

In diesem Fall hätten alle Tätigkeiten, die ausschließlich auf dem ersten kritischen Pfad liegen, einen "Kritikalitätsindex" von 0,6. Aktivitäten, die nur auf dem zweiten und dritten Pfad liegen, hätten einen Kritikalitätsindex von 0,25 bzw. 0,15. Eine Tätigkeit, die sowohl auf dem ersten als auch auf dem zweiten kritischen Pfad liegt, hätte einen Index von 0,85, usw.

Es gibt viele alternative Verteilungen, die für die Aktivitätsdauer in einer Monte-Carlo-Analyse verwendet werden können, von denen vier im Folgenden dargestellt werden:

 

 

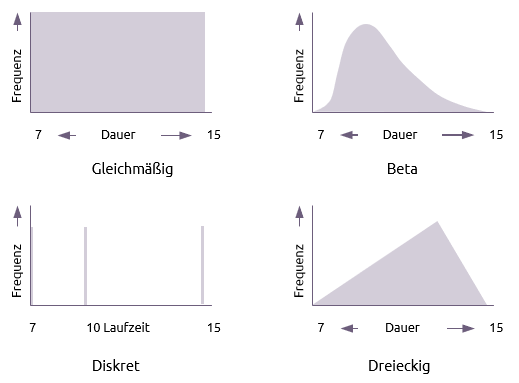
• Gleichmäßig

• Bei einer gleichmäßigen Verteilung hat jede Dauer innerhalb des Bereichs die gleiche Chance aufzutreten.

• Beta

• Diese Verteilung legt den Schwerpunkt auf die wahrscheinlichste Schätzung und wird in der PERT-Analyse verwendet

• Diskret

• Eine diskrete Verteilung listet die begrenzte Anzahl von Dauern auf, die die Aktivität haben kann. In diesem Fall könnte die Aktivitätsdauer entweder 7 oder 10 oder 15 sein und nichts anderes.

• Triangular

• Dadurch werden die drei Schätzungen gleich stark gewichtet. Die Formel zur Berechnung des Mittelwerts in dieser Verteilung lautet: