Normal precedence and activity-on-arrow network diagrams are known as deterministic networks. This is because the sequences of activities are determined by the person constructing the network. No allowance is made for alternative courses of action as the project progresses.
Multiple dependencies in deterministic networks only have one combined effect, known as an AND dependency. That means that activities A and B and C have to be complete before D can start.
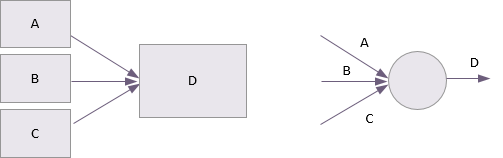
This simple assumption is not always sufficient to accurately model the true situation. Probabilistic dependencies provide the means of modelling much more complex relationships between activities. These are known as OR dependencies and they may be inclusive or exclusive.
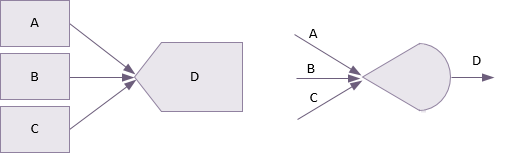
An inclusive OR dependency indicates that if any one of an activity’s predecessors is completed then the activity can start. In the precedence and activity-on-arrow examples below, activity D can start as soon as A or B or C is complete. This can be modified to indicate that any pair of activities must be completed for D to start.
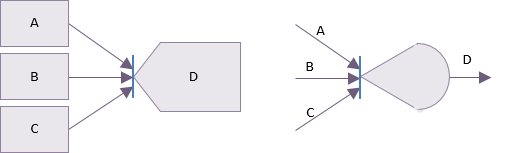
An exclusive OR dependency indicates that only one of the preceding activities can be undertaken. Whichever one is chosen excludes all others. The same type of rules can apply to outgoing activities as well as incoming activities. In an exclusive OR dependency, the occurrence of one task automatically excludes the occurrence of any other.
These basic dependencies can be enhanced in a variety of ways and provide means of producing network diagrams that model how activity dependencies may arise rather than how the planner assumes they will arise.
In contemporary planning, these techniques are primarily of academic interest only, since software packages that facilitate this kind of modelling and analysis are rare.





