Le schéma de priorités habituel et le diagramme d'activité fléchée sont connus comme des schémas déterministes. En effet, les séquences d'activités sont déterminées par le constructeur du schéma. Aucune allocation n’est faite pour d'autres plans d'action lorsque le projet progresse.
Des dépendances multiples dans les schémas déterministes ont seulement un effet combiné, connu sous le nom de la dépendance ET. Cela signifie que les activités A et B et C doivent être terminées avant que D ne puisse commencer.
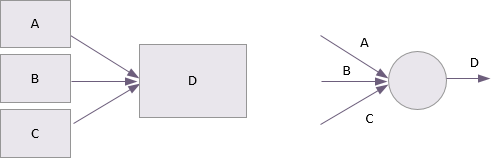
Cette hypothèse simple ne suffit pas toujours pour modéliser avec précision la situation réelle. Des dépendances probabilistes fournissent les moyens de modélisation de relations beaucoup plus complexes entre les activités. Ceux-ci sont connus sous le nom de dépendances OU et ils peuvent être inclusifs ou exclusifs.
Une dépendance OU inclusive indique que si l'un des prédécesseurs d'une activité est terminé alors l'activité peut commencer. Dans l'exemple de priorité et d'activité fléchée ci-dessous, l'activité D peut commencer dès que A ou B ou C est terminée. Cela peut être modifié pour indiquer que toute paire d'activités doit être remplie pour que D débute.
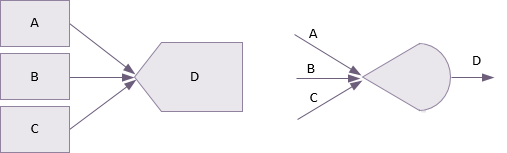
Une dépendance OU exclusive indique que seule une des activités précédentes peut être entreprise. Quelle que soit celle qui est choisie, cela exclut toutes les autres. Le même type de règle peut s'appliquer aux activités sortantes ainsi qu’aux activités entrantes. Dans la dépendance OU exclusive, l'apparition d'une tâche exclut automatiquement la survenance de tout autre.
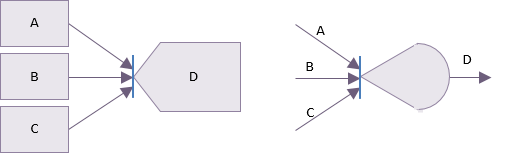
Ces dépendances de base peuvent être améliorées dans une variété de façons et fournissent des moyens de production de schémas d’ordonnancement qui modèlent comment les dépendances d'activités peuvent survenir plutôt que la façon dont le planificateur suppose qu'elles vont se poser.
Dans la planification contemporaine, ces techniques sont principalement d'intérêt académique, puisque les logiciels qui facilitent ce genre de modélisation et d'analyse sont rares.
Merci à la SMaP pour la traduction.





