El análisis de Monte Carlo usa un estimado a tres puntos de la duración de cada actividad in un diagrama de red. Entonces hace múltiple análisis de la ruta crítica para arribar a una gama de probabilidades del cronograma del proyecto.
La tabla aquí abajo muestra las duraciones estimadas a tres puntos para siete actividades.
| Tarea | Optimista | Más probable | Pesimista |
|---|---|---|---|
| A | 2 | 2 | 8 |
| B | 4 | 5 | 12 |
| C | 7 | 8 | 15 |
| D | 10 | 14 | 18 |
| E | 6 | 7 | 14 |
| F | 7 | 9 | 17 |
| G | 2 | 3 | 10 |
En practica, cada una de las actividades en la tabla mostrada aquí arriba puede tomar cualquier tiempo entre sus duraciones optimista y pesimista. Las dos redes mostradas aquí abajo hacen ver la diferencia entre los escenarios donde todas las actividades toman sus duraciones optimistas y donde todas toman sus duraciones pesimistas. Por claridad solo el paso hacia adelante del análisis de la ruta crítica es mostrado.
Escenario Optimista
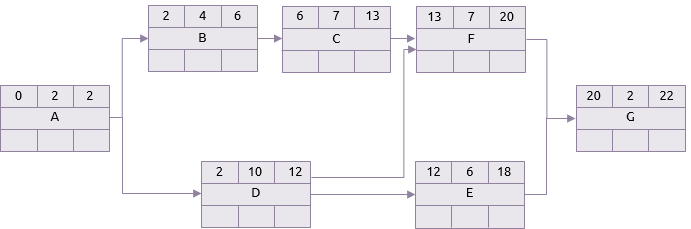
Escenario Pesimista
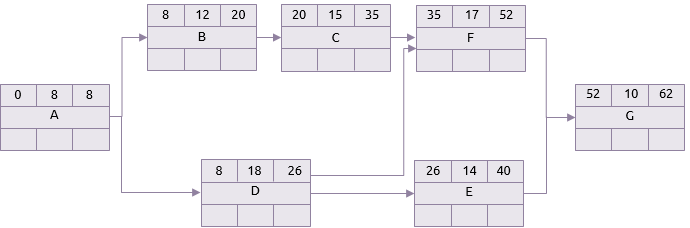
Este proyecto podría, por lo tanto, tomar cualquier tiempo entre 22 y 62 días pero estos dos extremos son los escenarios menos probables. Entre estos escenarios hay numerosos más. El análisis de Monte Carlo escoge duraciones al azar para cada tarea dentro de las gamas especificadas y entonces hace los análisis de la ruta crítica para cada conjunto de duraciones escogido.
Este ejercicio de análisis con diferentes duraciones puede hacerse cualquier número de veces pero paquetes de computador que apoyan este sistema generalmente recomiendan dar entre 250 - 1,000 iteraciones para lograr una distribución precisa de la duración del proyecto. Entre más complejo sea el proyecto habrá más distribución entre duraciones optimistas y pesimistas y más iteraciones serán requeridas.
Haciendo un gráfico de la frecuencia de cada posible duración, típicamente resulta en un gráfico como el que se muestra aquí abajo y que indica una distribución normal.
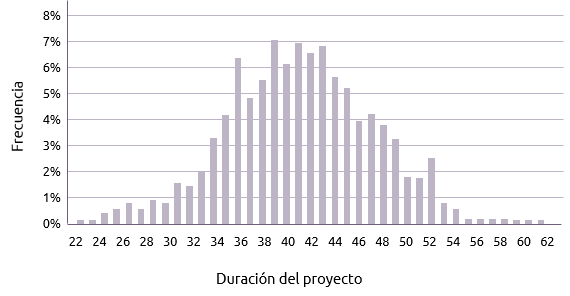
La duración media para el proyecto en cuestión, tomando la gráfica de distribución de duraciones parece ser aproximadamente 42 días. Esto significa hay que un 50% de posibilidades de terminar en 42 días.
Una indicación más exacta puede ser derivada dibujando la curva acumulada mostrada aquí abajo.
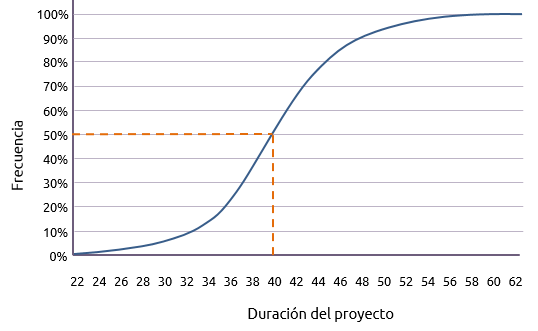
De todo esto, una variedad de preguntas pueden ser respondidas. Por ejemplo:
" ¿Que día hay un 50% de probabilidad de terminar?"
El grafico indica que la respuesta es el día 40 (al día más cercano).
A la inversa:
" ¿que probabilidad hay de finalizar el día 40?"
La respuesta, claro, es 50%
Habiendo hecho el análisis de Monte Carlo es improbable que haya una sola ruta crítica. Por lo tanto, es esencial conocer la criticidad de las actividades, i.e. la frecuencia con la cual ellas aparecen en la ruta crítica.
Si se hacen 1.000 iteraciones, puede ser que haya tres rutas críticas. La primera ocurre 600 veces, la segunda 250 veces y la tercera 150.
Si este fuese el caso, todas las actividades que ocurrieron exclusivamente en la primera ruta crítica tendrían un índice de criticidad de 0,6. Actividades que estuvieron solo en la segunda y tercera rutas críticas tendrían un índice de criticidad de 0,25 y 0,15 respectivamente. Una actividad que estuvo en la primera y segunda rutas criticas tendría un índice de criticidad de 0,85, y así seguido.
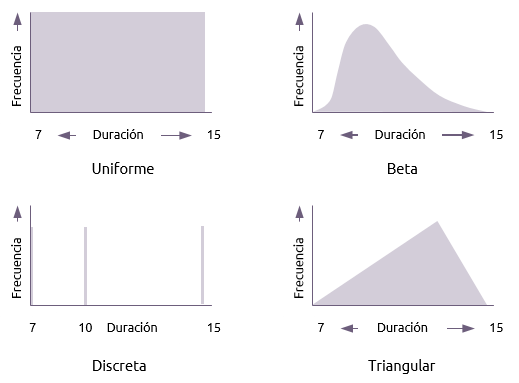
Hay muchas distribuciones alternativas que pueden ser utilizadas para las duraciones de actividades en el análisis de Monte Carlo, cuatro de ellas son mostradas aquí abajo:
-
Uniforme
Una distribución uniforme da a cualquier tiempo de duración en la gama, una probabilidad igual de ocurrir.
- Beta
-
Esta distribución coloca énfasis sobre el estimado tiempo de duración más probable y es la usada en el análisis llamando “Program Evaluation and Review Technique (PERT)”.
- Discreta
-
Una distribución discreta enlista un número limitado de tiempo de duración que la actividad podría tener. En este caso el tiempo de duración de la actividad puede ser o 7 o 10 o 15 días y nada más.
- Triangular
-
Esta distribución coloca énfasis en tres estimaciones. La fórmula para calcular la media en esta distribución es:
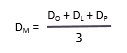
Gracias a Ignacio Manzanera por la traducción





