L’analisi Monte Carlo utilizza una stima della durata basata su tre livelli per ogni attività in un diagramma reticolare. Si eseguono poi multiple analisi del cammino critico per arrivare ad una serie di probabilità per la pianificazione del progetto.
La tabella seguente mostra le stime basate su tre livelli per sette attività.
| Attività | Durata ottimistica | Durata più probabile | Durata pessimistica |
|---|---|---|---|
| A | 2 | 2 | 8 |
| B | 4 | 5 | 12 |
| C | 7 | 8 | 15 |
| D | 10 | 14 | 18 |
| E | 6 | 7 | 14 |
| F | 7 | 9 | 17 |
| G | 2 | 3 | 10 |
In pratica, ciascuna delle attività nella tabella di cui sopra potrebbe avere una qualsiasi durata tra le sue previsioni di durata ottimistiche e pessimistiche. I due network che seguono mostrano la differenza tra uno scenario in cui tutte le attività impiegano la loro rispettiva durata ottimistica e uno in cui tutte le attività si protraggono per quanto previsto dalla loro durata pessimistica. Per chiarezza viene mostrato solo il forward pass dell’analisi del cammino critico.
Scenario ottimistico
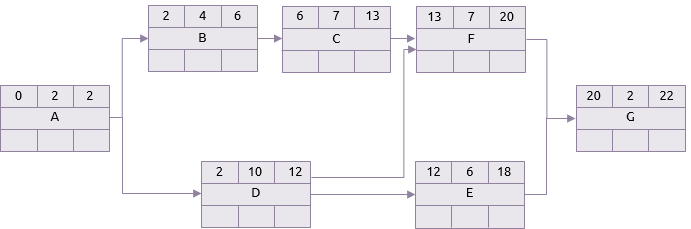
Scenario pessimistico
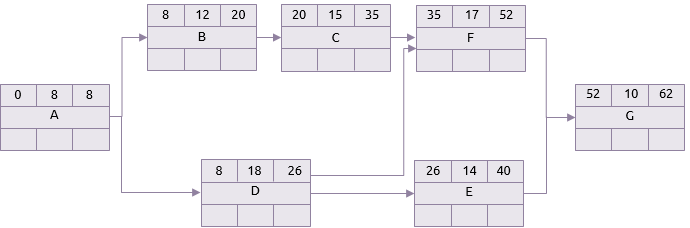
Questo progetto potrebbe, quindi, avere una durata qualsiasi tra 22 e 62 giorni, ma questi due estremi sono gli scenari più improbabili. In mezzo ci sono numerose altre possibili durate. L’analisi Monte Carlo sceglie in modo casuale le durate per ogni attività da intervalli specificati, e quindi esegue un’analisi del cammino critico.
Ciò può essere fatto qualsiasi numero di volte, e i pacchetti informatici che supportano quest’attività generalmente suggeriscono che 250 – 1.000 iterazioni daranno un’idea accurata della durata del progetto. Più complesso è il progetto, maggiore è la differenza tra le durate ottimistiche e pessimistiche, più saranno necessarie altre iterazioni.
Tracciare la frequenza di ogni possibile durata del progetto, in genere si traduce in una distribuzione approssimativamente normale.
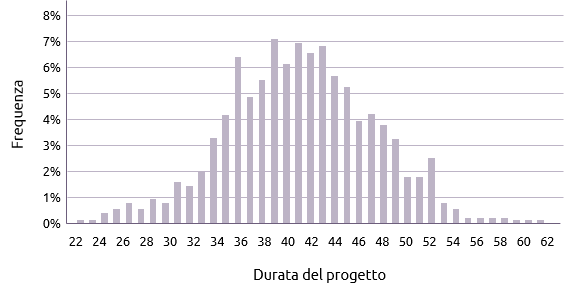
La durata media per il progetto, dal grafico qui sopra, sembra essere circa 42 giorni. Ciò significa che c’è una probabilità del 50% di finire il giorno 42.
Un’indicazione più precisa può essere ottenuta tracciando la curva cumulativa mostrata qui sotto.
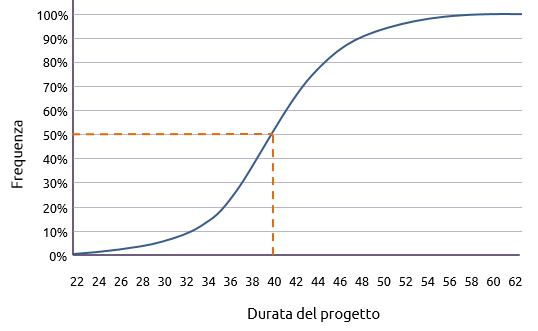
Da ciò, si può rispondere ad una gamma di domande. Per esempio:
“In quale giorno è c’è una probabilità di finire del 50%?”
Il grafico indica che la risposta è il giorno 40 (rispetto al giorno più vicino).
Viceversa:
“Che possibilità c’è di finire il giorno 40?”
La risposta, naturalmente, è che v’è una possibilità del 50%
Avendo effettuato l’analisi Monte Carlo è improbabile che ci sia un unico cammino critico. E’ quindi essenziale conoscere la ‘criticità’ delle attività, cioè la frequenza con cui compaiono su un cammino critico.
Se sono state fatte 1.000 iterazioni, può essere che ci siano tre possibili cammini critici. Il primo si verifica 600 volte, il secondo 250 volte e il terzo 150.
Se così fosse, tutte le attività che si sono verificate esclusivamente sul primo percorso critico avrebbero un ‘indice di criticità’ di 0,6. Le attività che erano solo sul secondo e sul terzo cammino critico avrebbero indici di criticità di 0,25 e 0,15 rispettivamente. Un’attività che era sia sul primo che sul secondo cammino critico avrebbe un indice di 0,85, e così via.
Ci sono molte distribuzioni alternative che possono essere utilizzate per la durata delle attività in un’analisi Monte Carlo, di cui quattro sono riportate di seguito:
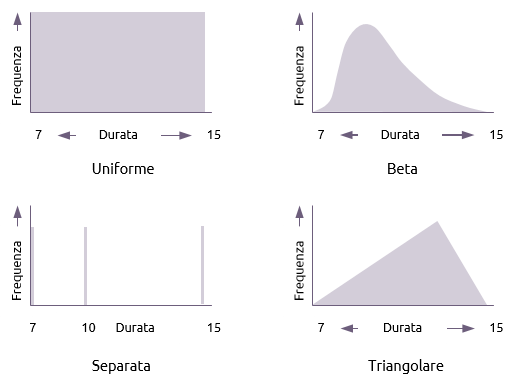
- Uniforme
-
Una distribuzione uniforme dà a qualsiasi durata nella gamma la stessa probabilità di verificarsi.
- Beta
-
Questa distribuzione pone l’accento sulla stima più probabile ed è quella usata nell’analisi PERT.
- Separata
-
Una distribuzione separata elenca il numero limitato di durate che l’attività potrebbe avere. In questo caso la durata dell’attività potrebbe essere o 7 o 10 o 15 e nessun’altra.
- Triangolare
-
Questo pone uguale enfasi su tre stime. La formula per il calcolo della media in questa distribuzione è:
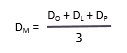
Grazie ad E-quality Italia per la traduzione





