L'analyse Monte-Carlo utilise une estimation en trois points de la durée de chaque activité dans un schéma d’ordonnancement. Elle effectue ensuite multiples analyses de chemin critique pour arriver à une gamme de probabilités pour un échéancier de projet.
Le tableau ci-dessous montre les trois estimations ponctuelles pour sept activités.
| Tâches | Optimiste | Très probable | Pessimiste |
|---|---|---|---|
| A | 2 | 2 | 8 |
| B | 4 | 5 | 12 |
| C | 7 | 8 | 15 |
| D | 10 | 14 | 18 |
| E | 6 | 7 | 14 |
| F | 7 | 9 | 17 |
| G | 2 | 3 | 10 |
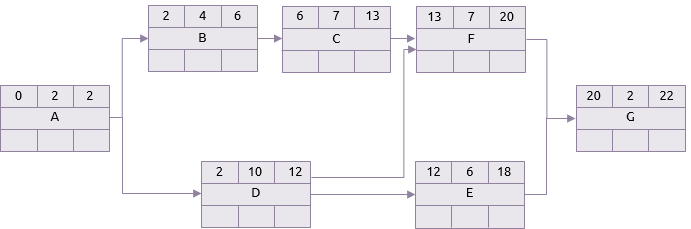
En pratique, n’importe laquelle des activités dans le tableau ci-dessus peut choisir n’importe quoi entre ses durées optimistes et pessimistes. Les deux schémas ci-dessous montrent la différence entre un scénario dans lequel toutes les activités ont leurs durées optimistes et celui où elles prennent toutes leurs durées pessimistes. Pour plus de clarté, seule la passe avant de l'analyse du chemin critique est affichée.
Scénario optimiste
Scénario pessimiste
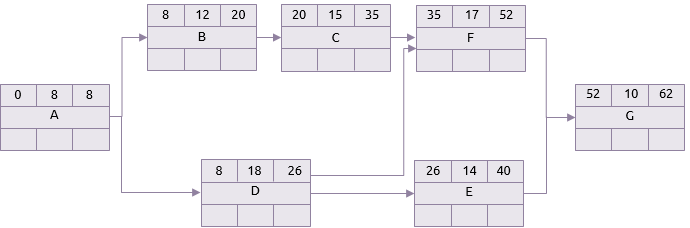
Ce projet pourrait, par conséquent, prendre tout simplement entre 22 et 62 jours, mais ces deux extrêmes sont les scénarios les plus improbables. Entre les deux, il a de nombreux autres. L'analyse Monte-Carlo choisit au hasard des durées pour chaque tâche à partir des plages spécifiées, puis effectue une analyse du chemin critique.
Cela peut être fait un certain nombre de fois et les logiciels qui soutiennent cela recommandent généralement que de 250 - 1000 itérations donneront une distribution précise pour la durée du projet. Plus complexe est le projet et plus grand est l'écart entre les durées optimistes et pessimistes, et plus d'itérations seront nécessaires.
Tracer la fréquence de la durée possible de chaque projet se traduit généralement par une distribution à peu près normale.
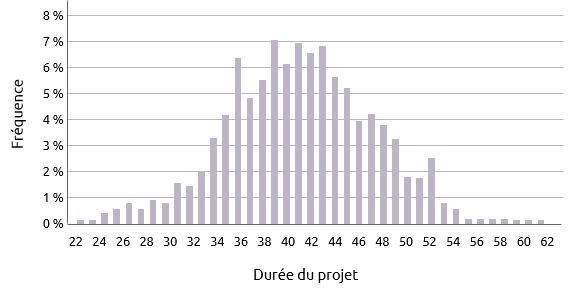
La durée moyenne pour le projet, à partir du graphique ci-dessus, semble être d'environ 42 jours. Cela signifie qu'il y a 50 % de chance de finir au jour 42.
Une indication plus précise peut être obtenue en traçant la courbe cumulative indiquée ci-dessous.
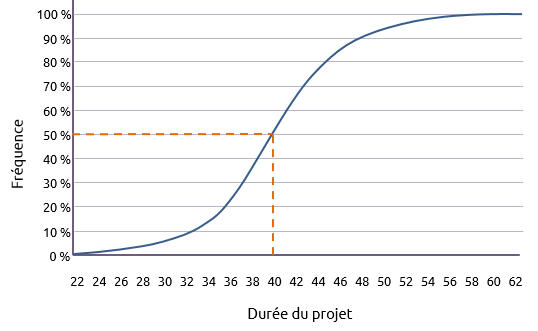
De là, une variété de questions peuvent trouver réponse. Par exemple :
« Sur quel jour avons-nous 50 % de chance d'avoir terminé? »
Le graphique indique que la réponse est de 40 jours (le jour le plus proche).
Inversement :
« Quelle est la chance que nous terminions au jour 40? »
La réponse, bien sûr, est 50 %
Ayant effectué une analyse de Monte-Carlo, il est peu probable qu'il y est un seul chemin critique. Il est donc essentiel de connaître la « criticité » des activités, à savoir la fréquence avec laquelle elles apparaissent sur un chemin critique.
Si 1000 itérations ont été effectuées, il se peut qu'il existe trois chemins critiques possibles. Le premier se produit 600 fois, le deuxième 250 fois et le troisième 150 fois.
Si tel est le cas, toutes les activités qui ont eu lieu exclusivement sur le premier chemin critique ont un « indice de criticité » de 0,6. Les activités qui se trouvent sur le deuxième et le troisième ont seulement des indices de criticité de 0,25 et 0,15 respectivement. Une activité qui est à la fois du premier et du second chemin critique a un indice de 0,85, et ainsi de suite.
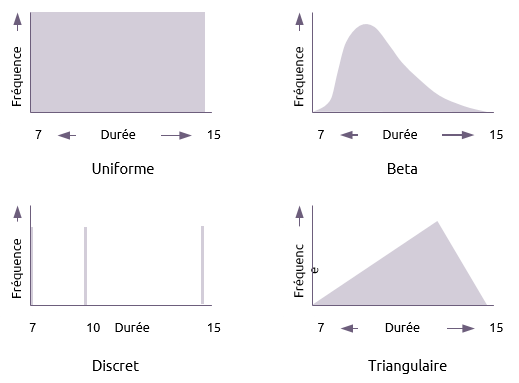
Il existe de nombreuses distributions alternatives qu'on peut utiliser pour les durées d'activité dans une analyse Monte-Carlo, dont quatre sont affichés ci-dessous :
-
Uniforme
Une distribution uniforme donne à toute durée de la plage une chance égale de se produire.
- Beta
-
Cette distribution met l'accent sur l'estimation la plus probable et est celle utilisée dans l'analyse PERT.
- Discrète
-
Une distribution discrète indique le nombre limité de durées que l'activité peut avoir. Dans ce cas, la durée de l'activité peut être soit 7 ou 10 ou 15 et rien d'autre.
- Triangulaire
-
Cela met un accent égal sur les trois estimations. La formule pour calculer la moyenne de cette distribution est la suivante :
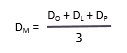
Merci à la SMaP pour la traduction.





