PERT es un acrónimo para la técnica de evaluación y revisión de programa, cuando el término programa representaba el cronograma de un proyecto más bien que un grupo de proyectos y cambio de negocio.
El análisis de la ruta crítica usa un estimado de punto simple para la duración de todas las actividades. En la realidad, es improbable que las duraciones de las actividades de un proyecto puedan ser estimadas con ese grado de exactitud. PERT usa un estimado de tres puntos para cada actividad. Los 3 estimados son conocidos como:
- optimista (muy improbable que la tarea tome menos tiempo que este);
- pesimista (muy improbable que la tarea tome más tiempo que esto);
- más probable (esto es lo que nosotros realmente pensamos que la tarea se tome).
La tabla aquí abajo muestra siete actividades con duraciones optimistas, pesimistas y más probables.
Tarea | Optimista | Más probable | Pesimista |
|---|---|---|---|
| A | 2 | 2 | 8 |
| B | 4 | 5 | 12 |
| C | 7 | 8 | 15 |
| D | 10 | 14 | 18 |
| E | 6 | 7 | 14 |
| F | 7 | 9 | 17 |
| G | 2 | 3 | 10 |
Usando las duraciones más probables en un análisis normal de la ruta crítica da un resultado mostrado aquí abajo con la ruta crítica en la secuencia: A, D, F, G.
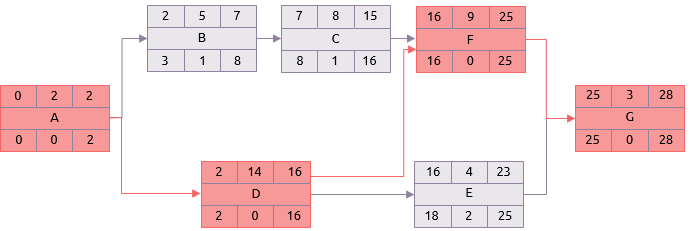
Sin embargo, las actividades actualmente tomaran cualquier tiempo entre los estimados optimista y pesimista. PERT usa estos estimados para calcular la duración media basada en la distribución beta.

O para mostrarlo más formalmente:

Por ejemplo, actividad B es más probable que se tome 5 días, pero hay una posibilidad de que podría tomarse 4 días o podría haber problemas que casuarina que se tomara tanto como 12 días.
Su duración media es por lo tanto:

Una tabla extendida mostrando las duraciones medias para cada actividad es mostrada aquí abajo:
Tarea | Optimista | Más Probable | Pesimista | Media |
|---|---|---|---|---|
| A | 2 | 2 | 8 | 3 |
| B | 4 | 5 | 12 | 6 |
| C | 7 | 8 | 15 | 9 |
| D | 10 | 14 | 18 | 14 |
| E | 6 | 7 | 14 | 8 |
| F | 7 | 9 | 17 | 10 |
| G | 2 | 3 | 10 | 4 |
Usando las duraciones medias en el análisis de la ruta crítica en vez de las estimaciones más probables da un resultado diferente.
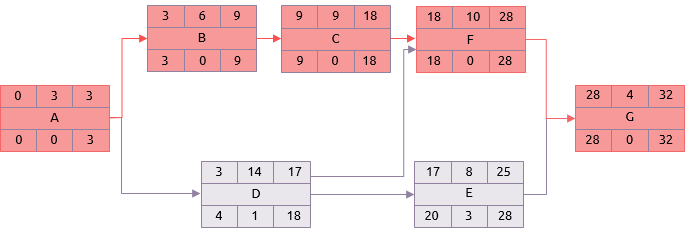
No solo la duración total del proyecto se incrementó a 32 días, pero la ruta crítica se ha movido. Ahora comprende las tareas A, B, C, F y G.
Aunque PERT usa tres estimados y por lo tanto es probable que de un resultado más realístico, pero el todavía provee un resultado único para la duración del proyecto. Este resultado descansa sobre una distribución normal y la desviación estándar (representada por la letra sigma) es usada para estimar la probabilidad de una gama de fechas de terminación.
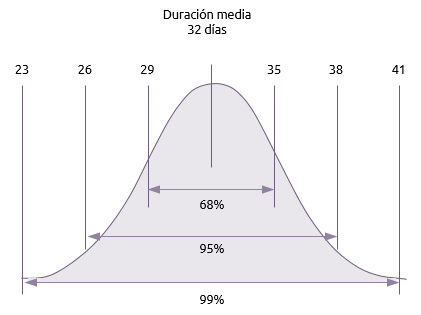
- 68% (Un-sigma)
-
Hay un 68% de probabilidad (68.27 para ser preciso) que el proyecto se tome más o menos una desviación estándar de la media, i.e. entre 32 – 3 (29 días) y 32 + 3 (35 días).
- 95% (Dos-sigma)
-
Hay un 95% de probabilidad (95.45 para ser preciso) que le proyecto se tome entre más o menos dos desviaciones estándar de la media, i.e. entre 32-3-3 (26 días) y 32+3+3 (38 días).
- 99% (Tres-sigma)
-
Hay un 99% de probabilidad (99.73 para ser preciso) que el Proyecto se tome entre más o menos tres desviaciones estándar de la media, i.e. entre 32-3-3-3 (23 días) y 32+3+3+3 (41 días).
Exactamente el mismo principio puede ser usado para gestionar con gamas de estimados de costo en vez de duraciones. PERT/Costo usa tres estimados de costo para cada actividad para calcular el costo medo para cada una de ellas. El costo medio total del proyecto es entonces la suma de todos los costos medios no solo aquellos que están en la ruta crítica.
PERT fue diseñado cuando el poder de las computadoras estaba escaso. Este tipo de análisis probabilístico es ahora normalmente ejecutado usando el análisis de Monte Carlo.
Gracias a Ignacio Manzanera por la traducción





