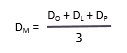蒙特卡罗分析法

蒙特卡罗分析对网络图中每个活动的持续时间进行三点估计。然后进行多个关键路径分析，以找到项目进度的概率范围。

下表列出了7项活动的三点估计。

 

任务	乐观	最可能	悲观
A	2	2	8
B	4	5	12
C	7	8	15
D	10	14	18
E	6	7	14
F	7	9	17
G	2	3	10

 

在实践中，上面表中的任何一个活动的持续时间都可能是介于乐观和悲观持续时间之间的某个值。下面的两个网络图显示了这两者情况的不同：一种情况是所有的活动都是其乐观的持续时间，另外一种情况是所有的活动都是悲观的持续时间。为了清晰起见，以下采用的是向前通道的关键路径分析。

 

乐观的情况

 

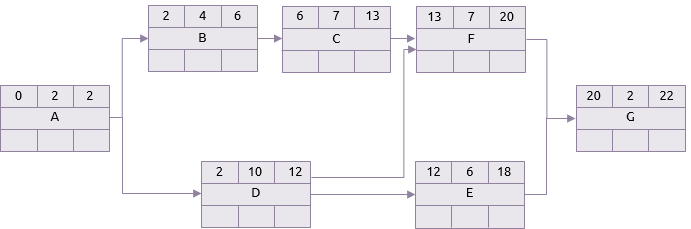
悲观的情况

 

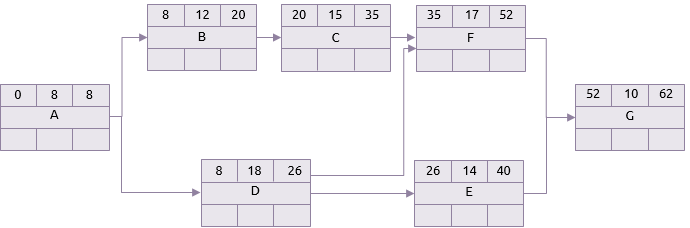
因此，这个项目的持续时间可能是22到62天之间某个值，但是，这两种是最不可能发生的极端情况。在这两者之间还有许多其他值。蒙特卡罗分析在一个指定范围内随机选择每个任务的持续时间，然后进行关键路径分析。

这可以做任意多次，计算机程序通常推荐250 - 1000次迭代计算，就可以计算出一个项目持续时间的准确分布。项目越复杂，乐观和悲观情况的持续时间分布就越广，就需要进行更多次的迭代计算。

绘制项目的每个可能持续时间的频率，通常的结果就是一种大致的正态分布。

 

 

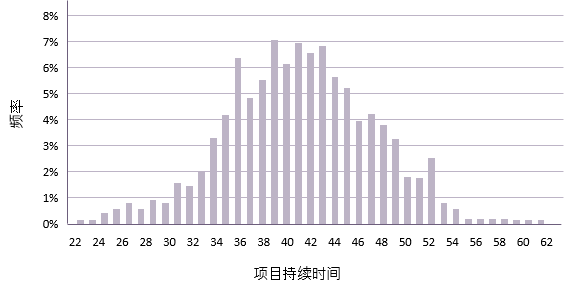
在上图中，这个项目的平均持续时间大约是42天。这意味着这个项目有50%的机会在第42天完成。

通过绘制下图所示的累积曲线，可以得到更准确的值。

 

 

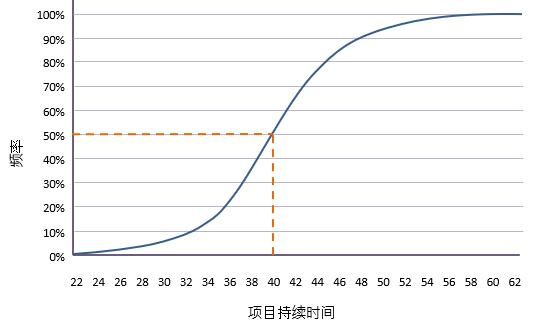
根据这张图，可以回答一系列的问题。例如：

“这个项目有50%的机会在哪一天完成?”

上面这张图表明答案是第40天（最接近的一天）。

反过来说：

“这个项目在第40天完成的机会是多少？”。

答案当然是50%

在进行蒙特卡罗分析时，不可能只有一条关键路径。因此，有必要了解活动的“关键性率”，也就是它们在关键路径上出现的频率。

如果进行了1000次迭代，可能有三条可能的关键路径。第一条出现了600次，第二条出现了250次，第三条出现了150次。

如果是这样的话，所有只在第一条关键路径上的活动都将具有0.6的“关键性率指数”。在第二条关键路径和第三条关键路径上的活动的“关键性率指数”分别是0.25和0.15。既在第一条关键路径又在第二条关键路径上的活动的“关键性率”是0.85，以此类推。

在蒙特卡罗分析中，活动的持续时间可能还有其他的分布，下图显示了其中的四种分布：

 

 

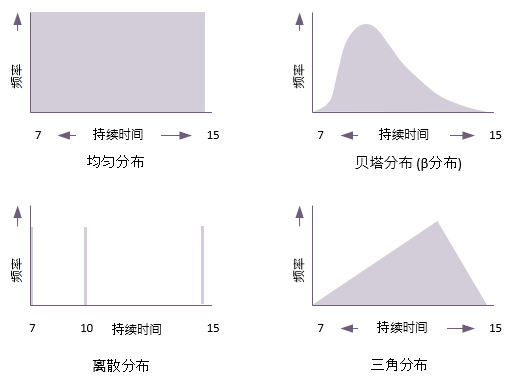
• 均匀分布

• 均匀分布使得一定范围内的任何持续时间都有相同的发生几率。

• 贝塔分布( β分布)

• 这种分布将重点放在最有可能的估计上，是在PERT计划评审技术中使用的方法。

• 离散分布

• 离散分布列出了一种活动可能的持续时间的有限数值。在这种情况下，活动持续时间可能是7或10或15，而不是其他。

• 三角分布

• 这种分布对三个估计强调了同等的重要性。在这种分布中，计算平均值的公式是：