Monte Carlo-analyse gebruikt een driepuntschatting van de duur van elke activiteit in een netwerkdiagram. Vervolgens voert het meerdere kritieke pad analyses uit om te komen tot een reeks kansen voor een projectplanning.
Onderstaande tabel geeft voor zeven activiteiten de driepuntschattingen weer.
Taak | Optimistisch | Hoogstwaar-schijnlijk | Pessimistisch |
|---|---|---|---|
A | 2 | 2 | 8 |
B | 4 | 5 | 12 |
C | 7 | 8 | 15 |
D | 10 | 14 | 18 |
E | 6 | 7 | 14 |
F | 7 | 9 | 17 |
G | 2 | 3 | 10 |
In de praktijk kan elk van de activiteiten in de bovenstaande tabel alles zijn tussen optimistische en pessimistische duur. De twee onderstaande netwerken laten het verschil zien tussen een scenario waarin alle activiteiten een optimistische en een pessimistische looptijd hebben. Voor alle duidelijkheid: alleen de voorwaartse doorgang van de analyse van het kritieke pad wordt getoond.
Optimistisch scenario
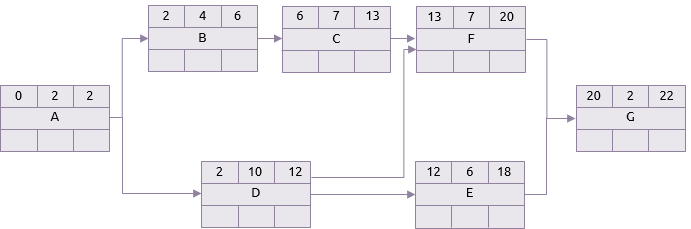
Pessimistisch scenario
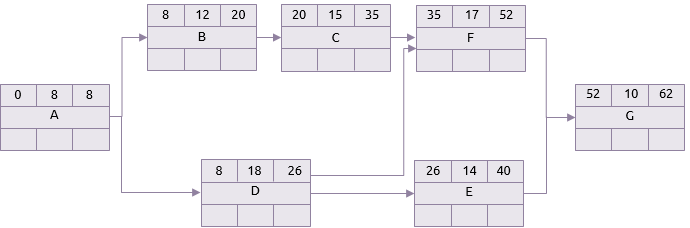
Dit project zou dus 22 tot 62 dagen in beslag kunnen nemen, maar deze twee uitersten zijn de meest onwaarschijnlijke scenario's. Daartussen zijn er nog vele andere. Monte Carlo-analyse kiest willekeurig de duur van elke taak uit de gespecificeerde selectie en voert vervolgens een kritieke pad analyse uit.
Dit kan een willekeurig aantal keren gedaan worden en computerpakketten die dit ondersteunen raden over het algemeen aan dat 250 - 1.000 iteraties een nauwkeurige verdeling zullen geven voor de duur van het project. Hoe complexer het project en hoe groter de spreiding tussen optimistische en pessimistische looptijden, hoe meer iteraties nodig zullen zijn.
Het plotten van de frequentie van elke mogelijke projectduur, resulteert meestal in een ruwe normaalverdeling.
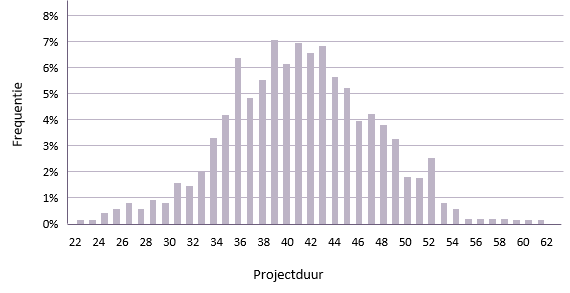
Uit bovenstaande grafiek blijkt dat de gemiddelde duur van het project ongeveer 42 dagen bedraagt. Dat betekent dat er 50% kans is om op dag 42 af te zijn.
Een nauwkeuriger indicatie kan worden afgeleid uit de hieronder getoonde cumulatieve curve.
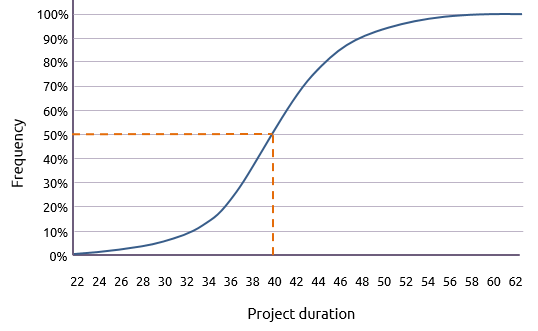
Hieruit kunnen verschillende vragen worden beantwoord. Bijvoorbeeld:
"Op welke dag is er een 50% kans dat het afgerond is?"
De grafiek geeft aan dat het antwoord dag 40 is (tot de dichtstbijzijnde dag).
Omgekeerd:
"Welke kans is er om op dag 40 af te ronden?"
Het antwoord is natuurlijk 50%.
Na het uitvoeren van de Monte Carlo-analyse is het onwaarschijnlijk dat er één kritisch pad is. Het is daarom van essentieel belang te weten wat de ’criticaliteit‘ van activiteiten is, d.w.z. de frequentie waarmee ze op een kritiek pad verschijnen.
Als 1.000 iteraties werden gedaan, kan het zijn dat er drie mogelijke kritieke wegen zijn. De eerste komt 600 keer voor, de tweede 250 keer en de derde 150 keer.
Als dit het geval zou zijn, zouden alle activiteiten die uitsluitend op het eerste kritieke pad optreden een 'criticaliteitsindex' van 0,6 hebben. Activiteiten die alleen op de tweede en derde optreden, zouden een criticaliteitsindex van respectievelijk 0,25 en 0,15 hebben. Een activiteit die zowel op het eerste als op het tweede kritieke pad was, zou een index van 0,85 hebben, enzovoort.
Er zijn veel alternatieve verdelingen die gebruikt kunnen worden voor de activiteitsduren in een Monte Carlo-analyse, waarvan er hieronder vier worden getoond:
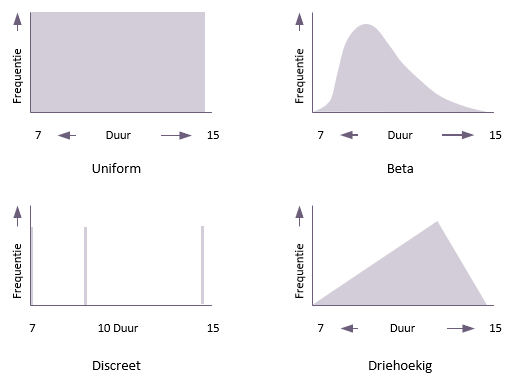
- Uniform
-
Een uniforme verdeling geeft elke tijdsduur in de reikwijdte een gelijke kans om voor te komen.
- Beta
-
Deze verdeling legt de nadruk op de meest waarschijnlijke schatting en wordt gebruikt in PERT analyses.
- Discreet
-
In een discrete verdeling wordt het beperkte aantal looptijden vermeld dat de activiteit zou kunnen hebben. In dit geval kan de duur van de activiteit 7 of 10 of 15 zijn en niets anders.
- Driehoekig
-
Dit legt evenveel nadruk op de drie ramingen. De formule voor het berekenen van het gemiddelde in deze verdeling is:
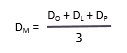
Met dank aan het BPUG-team voor de vertaling naar het Nederlands





