Analisis Monte Carlo menggunakan perkiraan tiga titik durasi untuk setiap aktivitas dalam diagram jaringan. Kemudian melakukan beberapa analisis jalur kritis untuk mencapai berbagai kemungkinan untuk jadwal proyek.
Tabel di bawah ini menunjukkan perkiraan tiga titik untuk tujuh kegiatan.
| Tugas | Optimis | Paling mungkin | Pesimis |
|---|---|---|---|
| A | 2 | 2 | 8 |
| B | 4 | 5 | 12 |
| C | 7 | 8 | 15 |
| D | 10 | 14 | 18 |
| E | 6 | 7 | 14 |
| F | 7 | 9 | 17 |
| G | 2 | 3 | 10 |
Dalam prakteknya, salah satu kegiatan dalam tabel di atas dapat mengambil apa pun di antara jangka waktu optimistik dan pesimisnya. Dua jaringan di bawah ini menunjukkan perbedaan antara skenario di mana semua kegiatan mengambil jangka waktu optimis mereka dan satu di mana mereka semua mengambil jangka waktu pesimis mereka. Untuk kejelasan, hanya forward pass dari analisis critical path yang ditampilkan.
Skenario Optimis
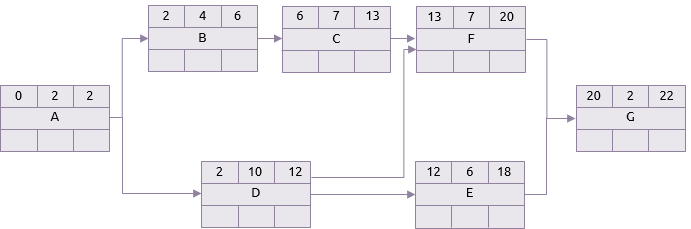
Skenario Pesimis
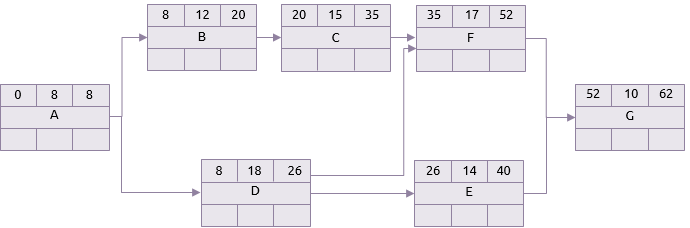
Oleh karena itu proyek ini bisa mengambil apa pun antara 22 dan 62 hari tetapi kedua ekstrem ini adalah skenario yang paling tidak mungkin. Di antara banyak lainnya. Analisis Monte Carlo secara acak memilih durasi untuk setiap tugas dari rentang yang ditentukan dan kemudian melakukan analisis jalur kritis.
Ini dapat dilakukan beberapa kali dan paket komputer yang mendukung ini umumnya menyarankan bahwa 250 - 1.000 iterasi akan memberikan distribusi yang akurat untuk durasi proyek. Semakin kompleks proyek dan semakin besar penyebaran antara jangka waktu optimis dan pesimis, semakin banyak iterasi yang diperlukan.
Merencanakan frekuensi dari setiap kemungkinan durasi proyek, biasanya menghasilkan distribusi yang kira-kira normal.
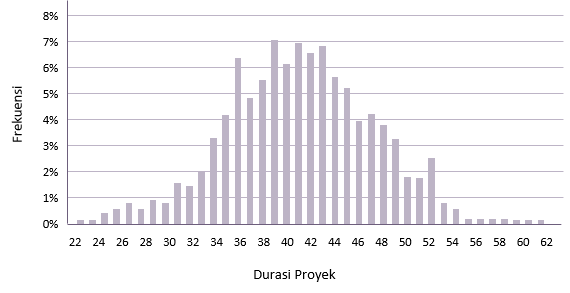
Durasi rata-rata untuk proyek, dari grafik di atas, tampaknya sekitar 42 hari. Itu berarti ada 50% peluang untuk menyelesaikan pada hari ke 42.
Indikasi yang lebih akurat dapat diperoleh dengan memplot kurva kumulatif yang ditunjukkan di bawah ini.
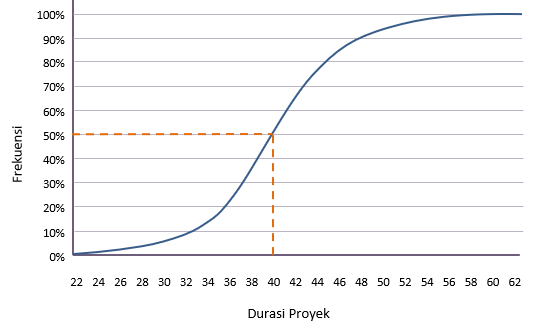
Dari sini, berbagai pertanyaan bisa dijawab. Sebagai contoh:
"Hari apa ada 50% kesempatan untuk selesai?"
Grafik menunjukkan bahwa jawabannya adalah hari ke 40 (ke hari terdekat).
Sebaliknya:
"Kesempatan apa yang ada di penghujung hari ke 40?"
Jawabannya, tentu saja, adalah 50%
Setelah melakukan analisis Monte Carlo, tidak mungkin ada satu jalur kritis. Oleh karena itu penting untuk mengetahui 'kekritisan' kegiatan, yaitu frekuensi kemunculannya di jalur kritis.
Jika 1.000 iterasi dilakukan, mungkin ada tiga kemungkinan jalur kritis. Yang pertama terjadi 600 kali, yang kedua 250 kali dan yang ketiga 150.
Jika ini kasusnya, semua kegiatan yang terjadi secara eksklusif di jalur kritis pertama akan memiliki 'indeks kekritisan' 0,6. Kegiatan yang berada di kedua dan ketiga hanya akan memiliki indeks kekritisan masing-masing 0,25 dan 0,15. Kegiatan yang berada di jalur kritis pertama dan kedua akan memiliki indeks 0,85, dan seterusnya.
Ada banyak distribusi alternatif daripada yang dapat digunakan untuk durasi aktivitas dalam analisis Monte Carlo, empat di antaranya ditunjukkan di bawah ini:
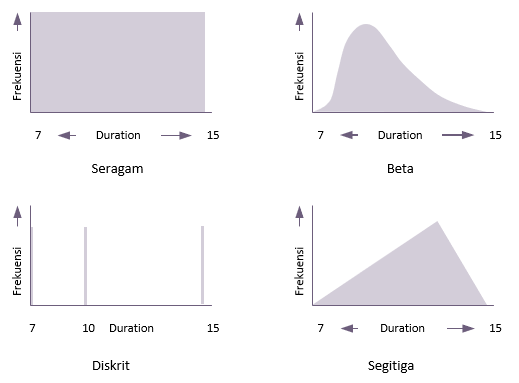
- Seragam
-
Distribusi yang seragam memberikan durasi yang sama dalam kisaran kesempatan yang sama untuk terjadi.
- Beta
-
Distribusi ini menempatkan penekanan pada perkiraan yang paling mungkin dan yang digunakan dalam analisis PERT.
- Diskrit
-
Distribusi diskrit mencantumkan sejumlah durasi terbatas yang dapat dimiliki oleh kegiatan tersebut. Dalam hal ini durasi aktivitas dapat berupa 7 atau 10 atau 15 dan tidak ada yang lain.
- Segitiga
-
Ini menempatkan penekanan yang sama pada tiga perkiraan. Rumus untuk menghitung mean dalam distribusi ini adalah:
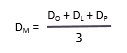
Terima kasih Valentinus Pramana untuk terjemahannya pada halaman ini.





