El método de la ruta crítica una técnica de cronograma para analizar un diagrama de red. El calcular las fechas cuando las actividades deben ocurrir e identifica flexibilidad en la ejecución de algunas actividades.
Las dos importantes limitaciones del análisis de la ruta crítica son:
- Solo una duración estimada es utilizada para cada actividad; y
- No tiene tolerancia para la disponibilidad de recursos.
El cálculo comprende tres fases:
- Paso hacia adelante;
- Paso hacia atrás; y
- Calculo de holguras.
El paso hacia delante calcula los tiempos tempranos cuando las actividades pueden ocurrir y al paso hacia atrás calcula los tiempos tardíos. La diferencia entre los dos indica el grado de flexibilidad que hay en la ejecución de la actividad y este es cuantificado como holgura.
Usando un computador, un modelo representado por el diagrama de red, puede ser ajustado y estos cálculos repetidos muchas veces y muy rápidamente. Esto permite que se puedan probar diferentes escenarios en lo que a menudo es llamado análisis ‘que-pasa-si’.
Cada actividad en el diagrama de red tendrá siete elementos básicos:
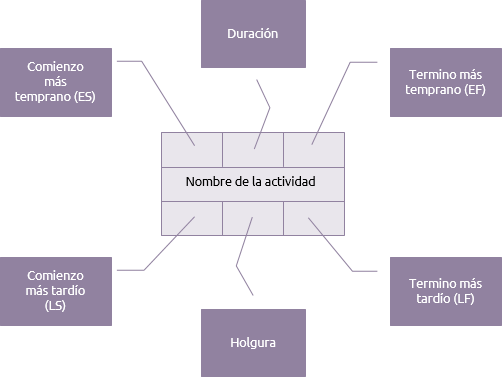
La duración es el tiempo requerido para completar la actividad. Las fechas arriba indicaran los tiempos más tempranos en que la actividad podría ser ejecutada y las fechas abajo indicaran los tiempos más tardíos a los cuales una actividad puede ser ejecutada.
El Paso hacia Adelante:
El paso hacia delante entonces empieza por colocar un cero como el comienzo más temprano para comenzar la actividad A. Como la duración de actividad A es 2 días, su terminado más temprano es el día 2. Si A es terminada el día 2 entonces este es el comienzo más temprano de las actividades B y D, entonces ese es el comienzo más temprano de B y D y así el cálculo continua.
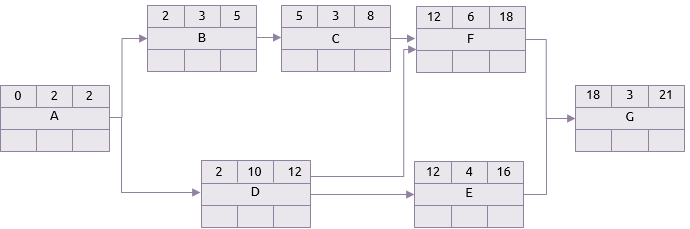
El próximo punto a notar es la actividad F. Esta actividad tiene dos predecesores C y D. El termino temprano para C el día 8 y para D es el día 12. Por lo tanto el tiempo más temprano en que F puede comenzar es el día 12.
Siguiendo el cálculo a su conclusión, el tiempo más temprano para terminar G (y por lo tanto el Proyecto) es 21 días.
El paso hacia atrás:
La fecha más temprana para terminar el Proyecto es asumida que sea la más tardía también. El proceso es entonces repetido, pero en reversa.
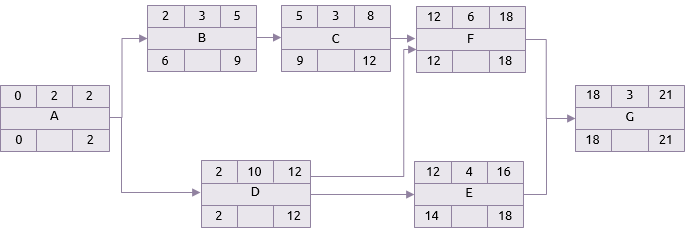
Si el fin más tardío para la actividad G es el día 21 y ella toma 3 días, su comienzo más tardío es por lo tanto el día 18. Esto significa que actividades F y E deben ser terminadas por el día 18 a más tardar.
El comienzo más tardío de actividad E es el día 14 y por lo tanto actividad D, quizás, tiene un final más tardío el día 14. Pero actividad D también tiene que ser terminada a tiempo para que actividad F pueda comenzar. El comienzo más tardío de actividad F es 12 y de aquí que actividad D tiene el final más tardío el día 12.
El mismo principio se aplica a la actividad A. Aunque la actividad B no tiene que empezar hasta el día 6, la actividad A debe terminar el día 2 porque es el día más tardío que actividad D puede comenzar.
Cálculos a Holgura:
La última fase es la más simple. Si hay una diferencia entre los tiempos más tempranos y los más tardíos en los que una actividad puede ejecutarse, ella tiene un grado de flexibilidad. Este es calculado substrayendo el comienzo más temprano del final más tardío. El resultado es el tiempo disponible para ejecutar la actividad. Deduciendo el tiempo requerido para ejecutar la actividad (i.e. la duración) del tiempo disponible, la holgura total es calculada.
Por ejemplo, en actividad B:
Tiempo disponible = final más tardío – comienzo más temprano (9 - 2)
Por tanto el tiempo disponible es días.
Holgura Total = tiempo disponible – duración (7 – 3)
Por lo tanto la actividad B tiene 4 días de holgura total i.e. puede ser demorada o extendida 4 días sin extender el final de la red de 21 días.
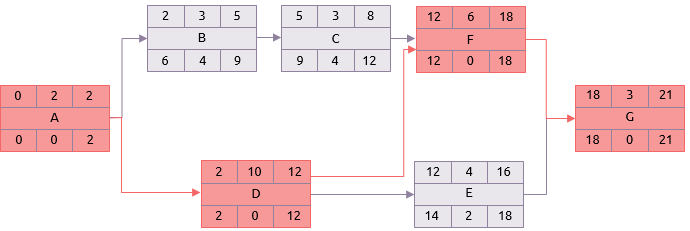
En algunas actividades el resultado será 0.
E.g. actividad D.
Holgura = Termino más tardío – Comienzo más temprano – duración
Estas son actividades críticas y su secuencia desde la primera hasta la última es la ruta crítica. En la red de ejemplo esta es:
A-D-F-G
La ruta crítica es la ruta más larga de la red y tiene la menor holgura (usualmente 0).
En este ejemplo simple, hay una sola ruta crítica con cero de holgura. i.e. hay una secuencia de actividades sin flexibilidad. Desde el punto de vista de la administración habrá inevitablemente muchas actividades con pequeñas cantidades de flexibilidad que tambien necesitan una atención cercana cuando se está controlando el proyecto.
En el ejemplo el enfoque estará en la ruta A, D, F y G, porque no tiene flexibilidad. Pero E solo tiene dos días de holgura y tambien necesita mucha atención.
Hay dos aspectos de la holgura que necesitamos mirar más cercanamente. Estos están demostrados en este ejemplo por las actividades B y C.
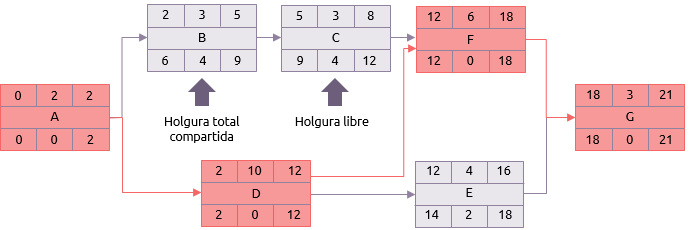
- Holgura total compartida:
-
Si B es demorada, tendrá un efecto de caída inmediato en C. Esto es normalmente referido como holgura total, aunque sería más exacto calificarlo como holgura total compartida.
- Holgura libre:
-
Holgura libre es la cantidad de tiempo por la cual una actividad demorada sin afectar ninguna de las actividades subsecuentes. Actividad C puede ser demorada hasta 4 días sin afectar nada porque F no puede empezar hasta el día 12 de todas formas.
El ejemplo usa solo dependencias comienzo-a-termino. El uso de otro tipo de dependencias hace el cálculo un poco más complejo y puede liderar a que las actividades tengan diferentes cantidades de holgura a su comienzo o final. Esto es más evidente en el análisis de escaleras.
Las fechas de comienzo y término de las actividades algunas veces están sujetos a restricciones diferentes de la lógica del diagrama de red. Estas están representadas por fechas impuestas.
Mas mejoras, principalmente por claridad cuando se presentan los resultados en una carta Gantt, se usan hitos y hamacas.
Las limitaciones del análisis de la ruta crítica con respecto al uso de una sola estimación de duración son tenidas en cuenta en técnicas como PERT y el análisis de Monte Carlo. Las limitaciones sobre disponibilidad de recursos son consideradas en extensiones de la técnica tales como la cadena crítica y el cronograma con limitación de recursos.
Gracias a Ignacio Manzanera por la traducción





