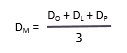A análise de Monte Carlo utiliza uma estimativa de três pontos da duração para cada atividade em um diagrama de rede. Em seguida, realiza múltiplas análises de caminho crítico para chegar a uma gama de probabilidades para um cronograma de projeto.
A tabela abaixo mostra as estimativas de três pontos para sete atividades.
| Tarefa | Otimista | Mais provável | Pessimista |
|---|---|---|---|
| A | 2 | 2 | 8 |
| B | 4 | 5 | 12 |
| C | 7 | 8 | 15 |
| D | 10 | 14 | 18 |
| E | 6 | 7 | 14 |
| F | 7 | 9 | 17 |
| G | 2 | 3 | 10 |
Na prática, qualquer uma das atividades da tabela acima poderia durar qualquer coisa entre suas durações otimista e pessimista. As duas redes abaixo mostram a diferença entre um cenário onde todas as atividades levam suas durações otimistas e um onde todas levam suas durações pessimistas. Para maior clareza, apenas o caminho de ida da análise do caminho crítico é mostrada.
Cenário otimista
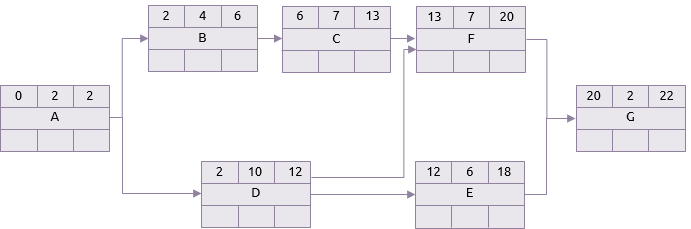
Cenário pessimista
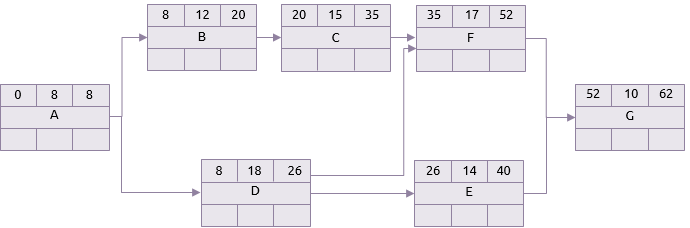
Este projeto poderia, portanto, levar entre 22 e 62 dias, mas estes dois extremos são os cenários mais improváveis. No meio há muitos outros. A análise Monte Carlo escolhe aleatoriamente as durações para cada tarefa a partir das faixas especificadas e depois realiza uma análise do caminho crítico.
Isto pode ser feito várias vezes e as ferramentas de computador que têm esta funcionalidade isto geralmente recomendam que 250 - 1.000 iterações dêem uma distribuição precisa para a duração do projeto. Quanto mais complexo for o projeto e quanto maior for a dispersão entre as durações otimista e pessimista, mais iterações serão necessárias.
A planificação da frequência de cada possível duração do projeto, normalmente resulta em uma distribuição mais ou menos normal.
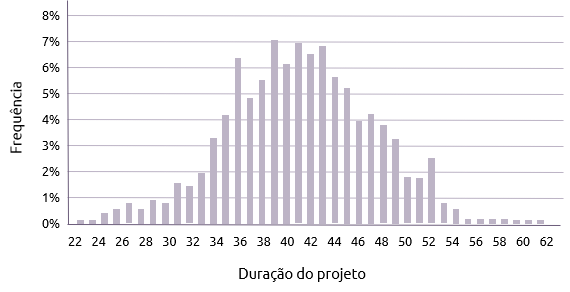
A duração média do projeto, pelo gráfico acima, parece ser de aproximadamente 42 dias. Isso significa que há 50% de chance de terminar até o 42º dia.
Uma indicação mais precisa pode ser obtida traçando a curva cumulativa mostrada abaixo.
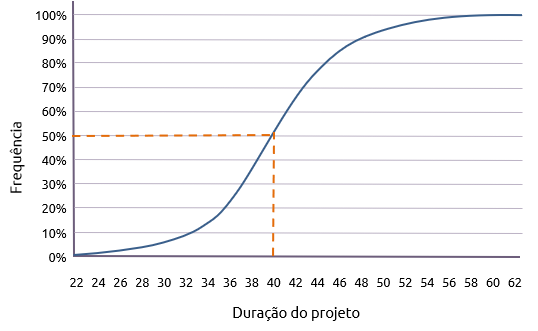
A partir disto, uma variedade de perguntas pode ser respondida. Por exemplo:
"Em que dia há 50% de chance de terminar?"
O gráfico indica que a resposta é o dia 40 (para o dia mais próximo).
Por outro lado:
"Que chance há de terminar no 40º dia?"
A resposta, é claro, é 50%.
Tendo realizado a análise de Monte Carlo, é pouco provável que haja um único caminho crítico. Portanto, é essencial conhecer a "criticidade" das atividades, ou seja, a frequência com que elas aparecem em um caminho crítico.
Se fossem feitas 1.000 iterações, talvez houvesse três caminhos críticos possíveis. O primeiro ocorre 600 vezes, o segundo 250 vezes e o terceiro 150 vezes.
Se este fosse o caso, todas as atividades que ocorreram exclusivamente no primeiro caminho crítico teriam um "índice de criticidade" de 0,6. As atividades que estavam no segundo e terceiro teriam índices de criticidade de 0,25 e 0,15, respectivamente. Uma atividade que estivesse tanto no primeiro quanto no segundo caminho crítico teria um índice de 0,85, e assim por diante.
Há muitas distribuições alternativas que podem ser usadas para a duração da atividade em uma análise de Monte Carlo, das quais quatro são mostradas abaixo:
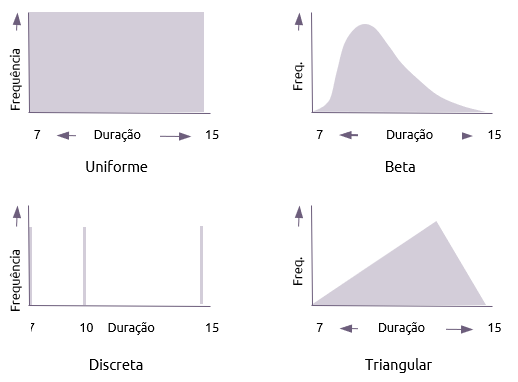
- Uniforme
-
Uma distribuição uniforme dá a qualquer duração na faixa uma chance igual de ocorrer.
- Beta
-
Esta distribuição coloca ênfase na estimativa mais provável e é a usada na análise PERT.
- Discreta
-
Uma distribuição discreta lista apenas o limitado número de durações que a atividade poderia ter. Neste caso, a duração da atividade poderia ser de 7 ou 10 ou 15 e nenhuma outra.
- Triangular
- Coloca a mesma ênfase nas três estimativas. A fórmula para calcular a média nesta distribuição é: