L'analyse du chemin critique est une technique de planification temporelle pour l'analyse d'un schéma d’ordonnancement. Elle calcule les dates où les activités du schéma devraient se produire et identifie la flexibilité dans l'exécution de certaines activités.
Les deux limites importantes de l'analyse du chemin critique sont les suivantes :
- une seule durée estimée est utilisée pour chaque activité;
- la technique ne tient pas compte de la disponibilité des ressources.
Le calcul comprend trois phases :
- progressif (passe avant);
- rétrograde (passe arrière);
- fluctuation.
Le calcul progressif estime le temps le plus tôt où les activités peuvent se produire et le calcul rétrograde calcule le temps le plus tard. La différence entre les deux indique le degré de flexibilité qu'il y a dans l'exécution de l'activité, ce qui est quantifié comme une fluctuation.
En utilisant un ordinateur, le modèle tel que représenté par le schéma d’ordonnancement peut être ajusté et ces calculs répétés maintes et maintes fois. Cela permet de tester différentes situations dans ce qui est souvent appelé l'analyse prédictive par simulation.
Chaque activité dans le schéma d’ordonnancement aura sept éléments de base :
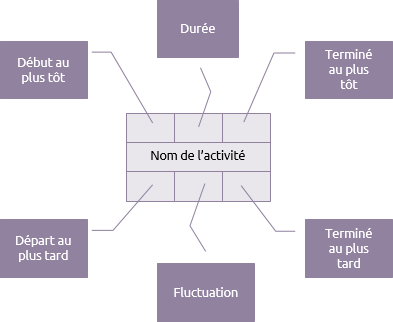
La durée est le temps nécessaire pour compléter l'activité. Les dates en haut indiqueront le temps le plus tôt que l'activité peut être débutée et les dates en bas indiquent le temps le plus tard que l'activité peut être achevée.
Le calcul progressif :
Le calcul progressif commence alors en plaçant 0 pour le début le plus tôt de l'activité A. Puisque sa durée est de 2 jours, le temps le plus tôt pour son arrivée est le jour 2. Si A est terminé au jour 2, alors cela est le début le plus tôt pour B et D, et donc le calcul se poursuit.
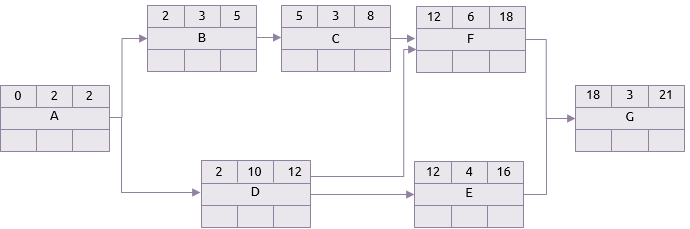
Le prochain point à noter est l'activité F. Cette activité a deux prédécesseurs : C et D. Le temps le plus tôt pour que C se termine est 8, mais pour D, c'est 12. Par conséquent, le temps départ le plus tôt pour F, est le jour 12.
En suivant le calcul jusqu'à sa conclusion, le temps le plus tôt pour que G se termine (et donc le projet) est de 21 jours.
Le calcul rétrograde :
Le temps le plus tôt pour que le projet se termine est supposé être aussi sa date de fin la plus tardive. Le processus est ensuite répété, mais en sens inverse.
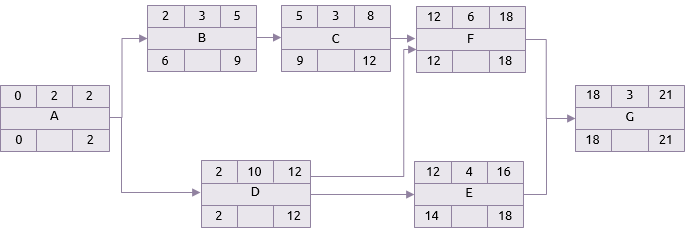
Si le temps le plus tard pour que G se termine est 21 jours, et que cela prend 3 jours, son temps de début sera donc le jour 18. Cela signifie que F et E doivent être terminés au plus tard au jour 18.
Le début le plus tard de E est le jour 14 et donc D doit aussi être terminé au plus tard le jour 14. Mais D doit aussi être terminé en temps pour le début de F. Le temps de début le plus tard de F est 12, et donc D doit être terminé au plus tard le jour 12.
Le même principe s'applique à A. Même si B ne commence pas avant le jour 6, A doit être terminé au jour 2, car c'est le début le plus tard auquel D doit commencer.
Calcul de fluctuation :
La dernière phase est la plus simple. S'il y a une différence entre le début le plus tôt et la fin le plus tard qu'une activité peut être faite, cela doit avoir un degré de flexibilité. Cela est calculé en prenant premièrement la date de début le plus tôt à partir du temps de fin le plus tard. Ce résultat est le temps disponible pour effectuer l'activité. En déduisant le temps nécessaire pour effectuer l'activité (à savoir la durée) à partir du temps disponible, la fluctuation totale (ou marge totale) est calculée.
Par exemple, sur l'activité B :
Temps disponible = temps de fin le plus tard - temps de début le plus tôt
= 9 - 2
Donc, le temps disponible est de 7 jours.
Fluctuation totale = temps disponible - durée
= 7 - 3
Donc l'activité B a une fluctuation de 4 jours, à savoir, elle peut être retardée ou prolongée de 4 jours sans excéder la date d’achèvement de 21 jours de l’ordonnancement.
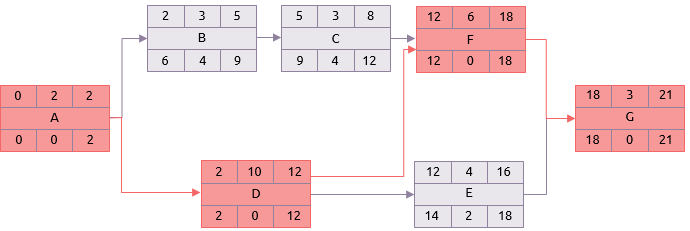
Pour certaines activités, le résultat sera de 0.
Par exemple, l'activité D :
Fluctuation = temps pour terminer le plus tard - temps de début le plut tôt - durée
= 12 – 2 – 10
= 0
Ce sont les activités critiques et la séquence de celles-ci de la première à la dernière activité est le chemin critique. Dans l'exemple de schéma, qui est :
A-D-F-G.
Le chemin critique est le plus long dans le schéma et a le moins de fluctuation (habituellement 0).
Dans cet exemple simple, il y a un seul chemin critique avec zéro fluctuation, à savoir, il y a une séquence d'activités sans flexibilité. D'un point de vue managérial, il y aura inévitablement de nombreuses activités avec de petites quantités de flexibilité qui ont besoin également d'une attention particulière lors du contrôle du projet.
Dans l'exemple, l'accent sera mis sur A, D, F et G, parce qu'ils n'ont pas de flexibilité. Mais E n'a une fluctuation que de 2 jours et doit également être surveillé attentivement.
Il y a deux aspects de fluctuation que nous devons examiner de plus près. Ceux-ci se manifestent par les activités B et C.
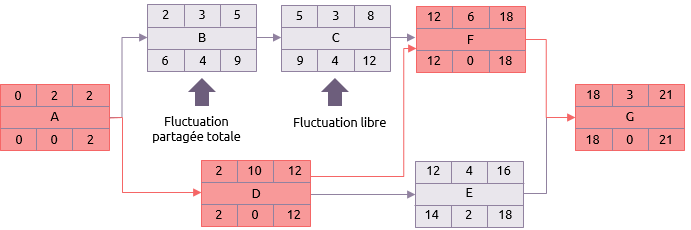
Fluctuation partagée totale :
Si B est retardé du tout, il aura une répercussion immédiate sur C. Cela est normalement juste appelé fluctuation totale, bien qu'il soit plus juste de la qualifier de fluctuation totale « partagée ».
Fluctuation libre :
La fluctuation libre est la quantité par laquelle une activité peut être retardée sans affecter les activités suivantes. Activité C peut être retardée jusqu'à 4 jours sans avoir de répercussion sur F, car elle ne peut débuter qu'au jour 23 de toute façon.
Le schéma exemple utilise uniquement les dépendances de type début-à-la-fin. L'utilisation d'autres types de dépendances de schéma d’ordonnancement rend le calcul un peu plus complexe et peut conduire à des activités ayant des quantités différentes de fluctuation à leur début ou fin. Cela est plus visible dans l'analyse des échelles.
Les dates de début et de fin des activités sont parfois soumises à des contraintes autres que la logique interne du schéma d’ordonnancement. Celles-ci sont représentées par des dates imposées.
D'autres améliorations, principalement par souci de clarté lors de la présentation des résultats de l'analyse du chemin critique dans un diagramme de Gantt, sont l'utilisation des jalons et des hamacs.
Les limites de l'analyse du chemin critique en ce qui concerne l'utilisation d'une seule estimation de la durée sont traitées dans des techniques telles que PERT et l'analyse de Monte-Carlo. Les limitations en ce qui concerne la disponibilité des ressources sont traitées dans des extensions de la technique telle que la chaîne critique et des planifications de ressources limitées.
Merci à la SMaP pour la traduction.





