关键路径分析是一种分析网络图的时间进度安排技术。它分析网络图中的活动应该发生的日期,识别某些活动执行中的灵活性。
关键路径分析的两个重要局限是:
- 每个活动只能有一个估计持续时间
- 这个技术没有考虑资源的可获得性
计算由三个阶段组成
- 向前通道
- 向后通道
- 时差计算
向前通道计算活动能发生的最早时间,向后通道计算发生的最晚时间。这两者的不同表明了在活动执行中所具有的灵活性,它量化表现为自由时差。
使用计算机,由网络图表示的这一模型可以被调整,这些计算可以重复进行。这就是可以测试不同的情景的“如果-怎样”分析。
网络图中的每个活动具有7个基本元素。
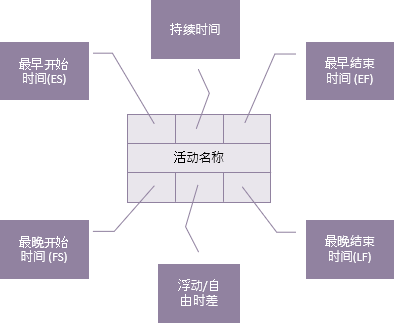
持续时间是完成这一活动所需要的时间。活动名称上面的时间是这一活动的最早时间,下面的时间是这一活动的最晚时间。
向前通道
在向前通道中,将活动A最早开始时间按照0来计算。因为它的持续时间是2天,它的最早完成时间是第2天。如果A在第2天完成的话,这就是活动B和D的最早开始时间,计算就可以这样继续下去。
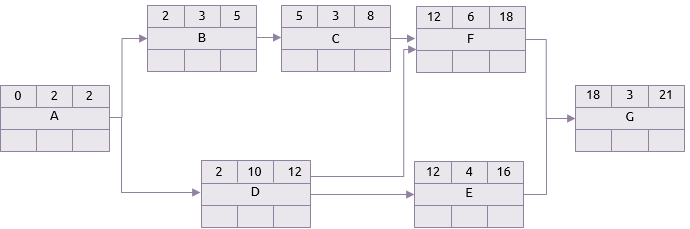
下一个需要注意的是活动F。它有两个前序活动C和D。C的最早完成时间是8,但是D的最早完成时间是12,因此,活动F最早可以开始的时间是第12天。
按照这样的计算,就可以得到结论,活动G的(也就是这个项目的)最早完成时间是第21天。
向后通道
项目的最早完成时间假定也是项目最晚完成时间。重复进行这个过程,但是相反方向。
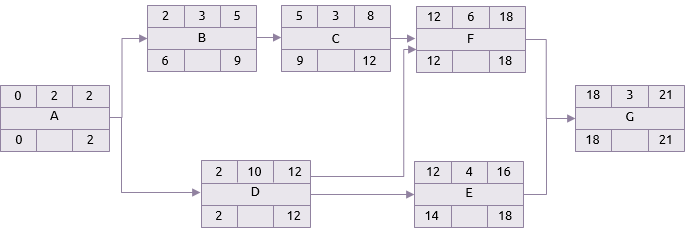
如果G的最晚在第21天完成,它的持续时间是3天,因此,它的最晚开始时间就是第18天。这表明活动F和E必须最晚在第18天完成。
活动E的最晚开始时间是14,因此活动D的最晚完成时间可能是14。但是活动D必须按时完成,这样活动F才能开始。活动F的最晚开始时间是12,因此,活动D的最晚完成时间是12。
同样的原理可以应用于活动A。尽管活动B可以直到第6天才开始,但活动A必须在第2天完成,因为这是活动D最晚可以开始的时间。
时差计算
最后一个阶段是最简单的。如果一个活动的最早时间和最晚时间之间有不同,这个活动就有一定程度的灵活性。用最晚完成时间减去最早开始时间,就是完成这一活动可以使用的时间。再减去活动所需要的持续时间,总的时差(总的浮动时间)就是可以计算出来。
例如,对于活动B:
可以使用的时间=最晚完成时间-最早开始的时间(9-2)。
因此可以使用的时间是7天。
总的时差=可以使用时间-持续时间(7-3)。
因此,活动B有4天总的时差,也就是说它可以延误或者延伸4天而对21天的网络活动完成时间没有影响。
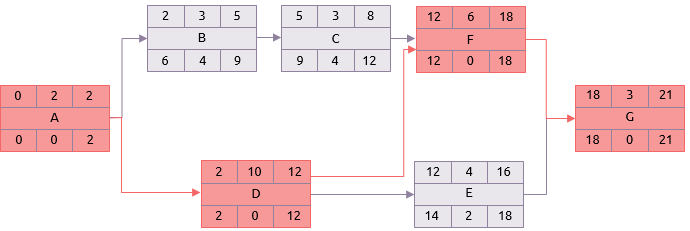
有一些活动,这个结果是0。
例如,活动D。
时差=最晚完成-最早开始-持续时间(12-2-10)。
这些是关键活动,这些关键活动从第一个到最后一个的顺序就组成了关键路径。在这个示例网络图中就是:
A-D-F-G。
关键路径是网络图中最长的、时差也最少(通常是0)的路径。
在示例中,只有一条时差是0的关键路径,也就是说这些活动都是没有灵活性的。从管理的角度来说,将不可避免的有很多具有少量灵活性的活动,在项目管控中也需要密切关注。
在这个示例中,关注的重点是活动A、D、F和G,因为他们没有灵活性。但是活动E只有2天的时差,也需要密切关注。
时差有两个方面我们需要仔细监控。这体现在活动B和C中。
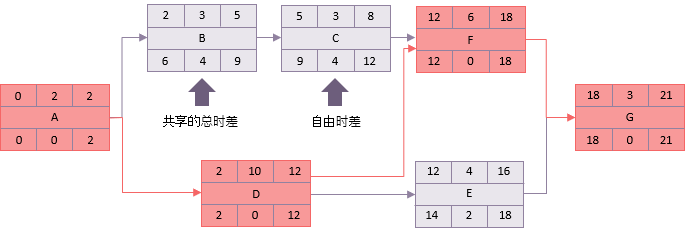
- 共享的总时差
-
如果活动B完全延误了,这将对活动C立即就有影响。这通常称为总时差,尽管更准确的应该将它定性为“共享的”总时差。
- 自由时差
- 自由时差是一个活动可能延误但对后序活动没有影响的时间。活动C可以延误4天而对活动F没有影响,因为活动F直到第12天才能开始。
示例网络图仅仅使用了‘开始—完成’的依赖关系。使用其他类型的依赖关系将会使计算略加复杂,导致活动的开始和完成的时差有所不同。这在阶梯分析中更值得注意。
除了网络图的内在逻辑,活动的开始和完成日期有时受到限制条件的影响。这些由强制性日期来体现。
更进一步,主要为了更清晰,在甘特图中体现关键路径分析结果时,主要使用里程碑和hammocks活动。
使用单个估算持续时间的关键路径分析的局限性在PERT计划评审技术分析和Monte Carlo分析法得到解决。资源获得性的局限在关键链和资源约束进度规划等技术的扩展中得到解决。





