L’analisi del percorso critico è una tecnica di pianificazione del tempo per analizzare un diagramma reticolare. Tale tecnica calcola le date in cui si possano verificare le attività nel reticolo e identifica la flessibilità nello svolgimento di alcune attività.
I due importanti limiti dell’analisi del cammino critico sono che:
- è utilizzata una sola durata stimata per ciascuna azione;
- la tecnica non prevede margini per la disponibilità delle risorse.
Il calcolo comprende tre fasi:
- forward pass
- backward pass
- calcolo del float
Il forward pass calcola i primi tempi in cui si possono verificare le attività e il backward pass calcola i tempi più recenti. La differenza tra i due indica il grado di flessibilità che c’è nello svolgimento delle attività e questo è quantificato come float.
Utilizzando un computer, il modello così com’è rappresentato dal diagramma reticolare può essere regolato e questi calcoli possono essere ripetuti più e più volte. Questo permette di testare diverse situazioni in quella che viene spesso chiamata analisi ‘what-if’.
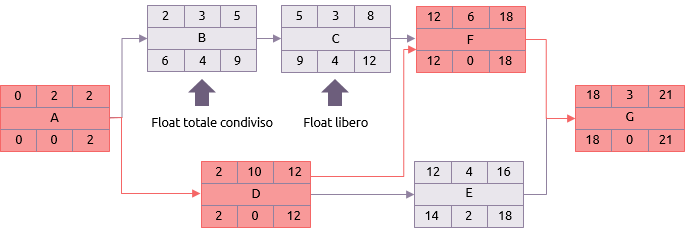
Ogni attività nel diagramma reticolare avrà sette elementi fondamentali:
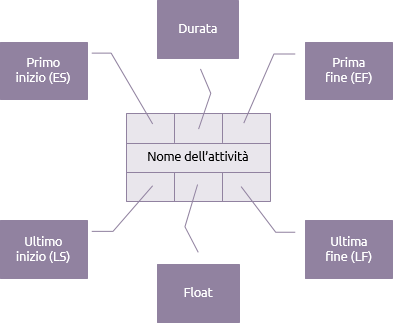
La durata è il tempo necessario per completare l’attività. Le date più in alto indicheranno la prima volta che l’attività possa essere svolta e le date più in basso indicheranno l’ultima volta che l’attività possa essere eseguita.
Il forward pass
Il passo in avanti poi inizia ponendo 0 come il primo inizio dell’attività A. Dal momento che la sua durata è di 2 giorni il suo primo termine è il giorno 2. Se l’attività A è finita dal giorno 2 allora tale giorno diviene il primo inizio delle attività B e D, e così via.
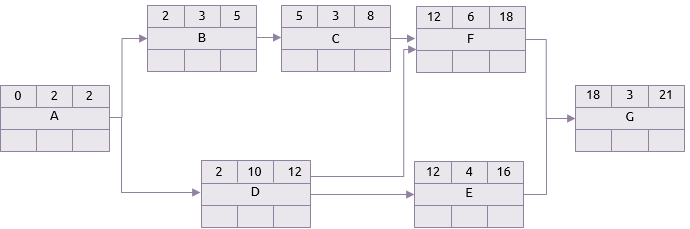
Il prossimo punto degno di nota è l’attività F. Questa attività ha due predecessori, le attività C e D. Il primo termine di C è il giorno 8 ma il primo termine di D è il giorno 12. Pertanto, la prima occasione in cui F può iniziare è il giorno 12.
Svolgendo il calcolo fino alla sua conclusione, il primo termine per l’attività G (e quindi per il progetto) è in 21 giorni.
Il backward pass
Il primo termine per il progetto si presume sia anche il suo termine ultimo. Il processo viene quindi ripetuto, ma in senso inverso.
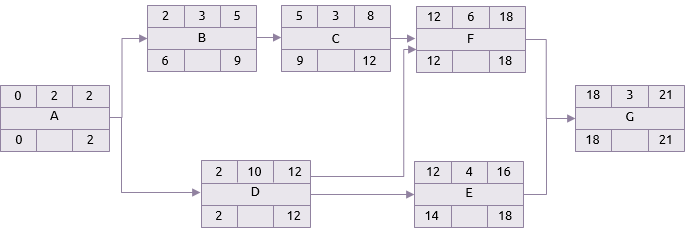
Se il termine ultimo di G è il giorno 21, e ci vogliono tre giorni, la sua ultima possibilità di partire è dunque il giorno 18. Ciò significa che le attività F ed E devono essere terminate al massimo il giorno 18.
L’ultima partenza per l’attività E è il giorno 14 e quindi D, magari, trova il suo termine ultimo nel giorno 14. Ma anche l’attività D deve essere completata in tempo per per iniziare la F. L’ultimo inizio possibile di F è il giorno 12 e quindi D ha un temine ultimo il giorno 12.
Lo stesso principio si applica all’attività A. Anche se B non deve iniziare fino al giorno 6, A deve essere completata entro il 2 perché è l’ultima occasione in cui D può iniziare.
Calcolo del Float:
L’ultima fase è la più semplice. Se vi è una differenza tra i primi e gli ultimi tempi in cui un’attività può essere svolta, tale attività deve avere quindi un certo grado di flessibilità; il quale grado di flessibilità è determinato prendendo la prima partenza dall’ultimo termine. Il risultato è il tempo disponibile per eseguire l’attività. Sottraendo il tempo necessario per eseguire l’attività (cioè la durata) dal tempo disponibile, il float totale (o ‘slack totale’) è calcolato.
Ad esempio, sull’attività B:
Tempo a disposizione = termine ultimo – inizio minimo (9-2)
Pertanto il tempo a disposizione è di 7 giorni.
Float totale = tempo a disposizione – durata (7-3)
Pertanto, l’attività B dispone di 4 giorni di float totale, vale a dire che potrebbe essere ritardata o prorogata di quattro giorni senza posticipare la data di fine reticolo fissata per il giorno 21.
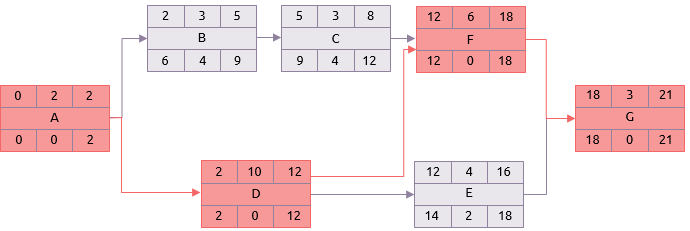
In alcune attività il risultato sarà 0.
Esempio: Attività D.
Float = termine ultimo – inizio minimo – durata (12-2-10)
Queste sono le attività critiche e la sequenza di queste attività dalla prima all’ultima è il cammino critico. Nel reticolo di esempio è:
A-D-F-G.
Il cammino critico è il percorso più lungo attraverso il reticolo ed ha il minor float (generalmente 0).
In questo semplice esempio vi è un unico percorso critico con float Zero, cioè vi è una sequenza di attività senza alcuna flessibilità. Da un punto di vista manageriale ci sono inevitabilmente molte attività con piccole quantità di flessibilità che richiedono anche molta attenzione quando si controlla il progetto.
Nell’esempio il focus sarà sulle attività A, D, F e G, perché non hanno flessibilità. Ma l’attività E ha solo due giorni di float e ha quindi bisogno anch’essa di essere osservata con attenzione.
Ci sono due aspetti di float che abbiamo bisogno di guardare più da vicino. Questi sono dimostrati dalle attività di B e C.
-
Float totale condiviso
-
Se B è del tutto in ritardo, avrà un immediato effetto domino sull’attività C. Questo è normalmente indicato soltanto come float totale, anche se sarebbe più corretto qualificarlo come float totale ‘condiviso’.
-
Float libero:
- Il float libero è l’ammontare di tempo entro cui un’attività può essere ritardata senza compromettere alcuna delle attività successive. L’attività C può essere ritardato fino a 4 giorni senza avere alcun effetto domino, perché F non può comunque iniziare fino al giorno 12.
Il reticolo di esempio utilizza solo dipendenze start-to-finish. L’utilizzo di altri tipi di dipendenze nei diagrammi reticolari rendono il calcolo leggermente più complesso e può portare ad attività con diverse quantità di float al loro inizio o al loro termine. Questo è più evidente nell’analisi delle scale.
Le date di inizio e di fine delle attività a volte sono soggette a vincoli piuttosto che alla logica interna del diagramma reticolare. Questi vincoli sono ad esempio le scadenze imposte.
Ulteriori miglioramenti, soprattutto per la chiarezza della presentazione dei risultati delle analisi del cammino critico in un diagramma di Gantt, consistono nell’utilizzo di milestones e hammocks.
I limiti dell’analisi del cammino critico per quanto riguarda l’uso di una sola previsione di durata sono valicati tramite tecniche come la PERT e l’analisi di Monte Carlo. Le limitazioni per quanto riguarda la disponibilità di risorse sono risolte nelle estensioni dell’applicazione della tecnica, come la catena critica e il pianificazione delle risorse limitate.
Grazie ad E-quality Italia per la traduzione





