Kritieke pad analyse is een tijdsplanningstechniek voor het analyseren van een netwerkdiagram. Het berekent datums waarop activiteiten in het netwerk moeten plaatsvinden en identificeert flexibiliteit in de uitvoering van sommige activiteiten.
De twee belangrijke beperkingen van kritieke pad analyse zijn dat:
- voor elke activiteit slechts één geschatte duur gebruikt wordt;
- de techniek geen rekening houdt met de beschikbaarheid van resources.
De berekening bestaat uit drie fasen:
- forward pass (voorwaardse berekening)
- backward pass (achterwaardse berekening)
- float (spelingberekeningen) .
De 'forward pass' berekent de vroegste momenten waarop activiteiten kunnen plaatsvinden en de 'backward pass' berekent de laatste momenten. Het verschil tussen beide geeft de mate van flexibiliteit aan in de uitvoering van de activiteit en wordt gekwantificeerd als speling (float).
Met behulp van een computer, kan het model zoals weergegeven in het netwerkschema, worden aangepast en kunnen deze berekeningen keer op keer worden herhaald. Hierdoor kunnen verschillende situaties worden getoetst in wat vaak 'what-if'-analyse wordt genoemd.
Elke activiteit in het netwerkschema bestaat uit zeven basiselementen:
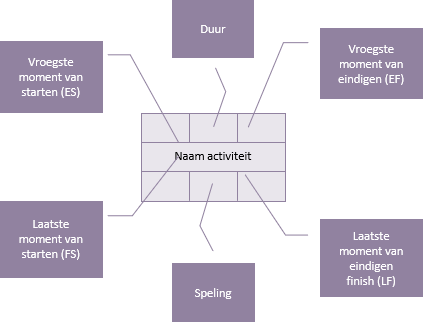
De duur is de tijd die nodig is om de activiteit te voltooien. De bovenste datums geven de vroegste tijd aan waarop de activiteit zou kunnen worden uitgevoerd en de onderste datums geven de laatste tijd aan waarop de activiteit zou kunnen worden uitgevoerd.
De forward pass:
De 'forward pass' begint dan met het plaatsen van 0 als de vroegste start van activiteit A. Aangezien de duur 2 dagen is, is dag 2 het vroegste einde. Als A op dag 2 klaar is, dan is dat de vroegste start van B en D, en gaat de berekening dus door.
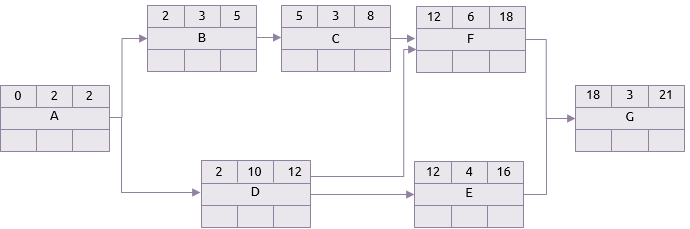
Het volgende punt om op te merken is activiteit F. Deze activiteit heeft twee voorgangers C en D. C's vroegste einde is 8, maar D's is 12. Het vroegste moment dat F kan beginnen is dus dag 12.
Na de berekening is het vroegste einde voor G (en dus het project) 21 dagen.
De backward pass:
Het vroegste einde van het project wordt verondersteld ook het laatste einde te zijn. Het proces wordt dan herhaald, maar in omgekeerde richting.
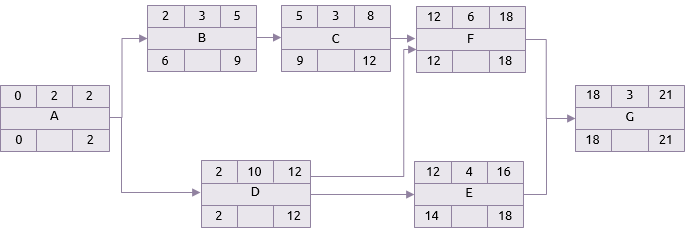
Als het laatste einde van G dag 21 is en het duurt 3 dagen, dan is de laatste start dus dag 18. Dit betekent dat F en E uiterlijk op dag 18 gereed moeten zijn.
E's laatste start is 14 en daarom heeft D misschien een laatste einde van 14. Maar D moet ook op tijd klaar zijn om F te laten starten. De laatste start van F is 12 en D heeft dus een laatste einde van 12.
Hetzelfde principe geldt voor A. Ook al hoeft B niet voor 6 te beginnen, A moet met 2 gereed zijn want dat is het laatste moment dat D kan beginnen.
Float berekeningen:
De laatste fase is de eenvoudigste. Als er een verschil is tussen het vroegste en het laatste moment dat een activiteit kan worden gedaan, moet er een zekere flexibiliteit zijn. Dit wordt berekend door eerst de vroegste start te nemen vanaf het laatste einde. Het resultaat is de beschikbare tijd om de activiteit uit te voeren. Door de tijd die nodig is om de activiteit uit te voeren (d.w.z. de duur) af te trekken van de beschikbare tijd, wordt de 'total float' (of 'totale speling') berekend.
Bijvoorbeeld over activiteit B:
Beschikbare tijd = laatste einde - vroegste start (9 - 2)
Daarom is de beschikbare tijd 7 dagen.
Total float = beschikbare tijd - duur (7 - 3)
Daarom heeft activiteit B een 'total float' van 4 dagen, d.w.z. dat deze met 4 dagen kan worden uitgesteld of verlengd zonder dat de einddatum van het netwerk van 21 dagen wordt verlengd.
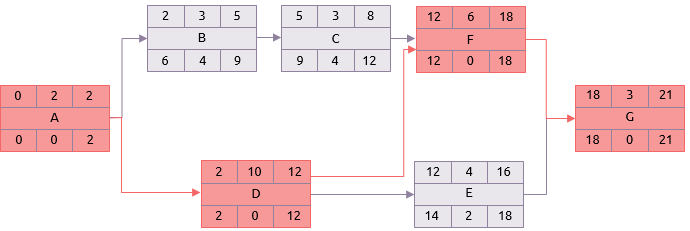
Voor sommige activiteiten zal het resultaat 0 zijn.
Bijvoorbeeld activiteit D.
Float (speling) = Laatste einde - vroegste start - duur (12-2-10)
Dit zijn de kritieke activiteiten en de volgorde van deze, van de eerste naar de laatste activiteiten, is het kritieke pad. In het voorbeeld netwerk is dat:
A-D-F-G.
Het kritieke pad is het langste pad door het netwerk en heeft de minste speling (meestal 0).
In dit eenvoudige voorbeeld is er één enkel kritiek pad met nul speling, d.w.z. er is een opeenvolging van activiteiten zonder flexibiliteit. Vanuit managementperspectief zullen er onvermijdelijk veel activiteiten zijn met een kleine mate van flexibiliteit, die ook veel aandacht nodig hebben bij het beheren van het project.
In het voorbeeld ligt de focus op A, D, F en G, omdat ze geen flexibiliteit hebben. Maar E heeft maar 2 dagen speling en moet ook goed in de gaten gehouden worden.
Er zijn twee aspecten van speling waar we nader naar moeten kijken. Deze worden gedemonstreerd door de activiteiten B en C.
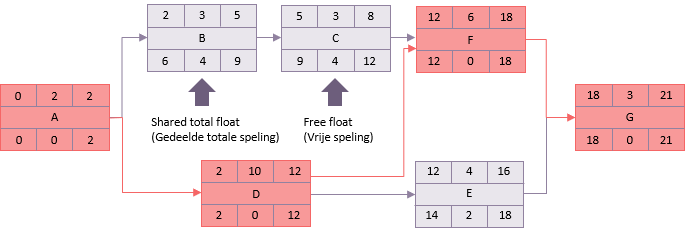
- Shared 'total float':
-
Indien B vertraging oploopt, zal dit een onmiddellijk effect hebben op C. Dit wordt gewoonlijk slechts aangeduid als 'total float' (totale speling), hoewel het nauwkeuriger zou zijn om het te kwalificeren als 'gedeelde' totale speling.
- Free float:
-
'Free float' (vrije speling) is het aantal dagen waarmee een activiteit kan worden vertraagd zonder dat dit van invloed is op latere activiteiten. Activiteit C kan tot 4 dagen worden vertraagd zonder dat een opschuif effect heeft, omdat F in ieder geval pas op dag 12 kan beginnen.
Het voorbeeldnetwerk maakt alleen gebruik van 'start-to-finish' afhankelijkheden. Het gebruik van andere soorten afhankelijkheden maakt de berekening iets complexer en kan leiden tot activiteiten met verschillende hoeveelheden speling aan het begin of einde. Dit is het meest merkbaar in de analyse van getrapte planning.
De begin- en einddatums van activiteiten zijn soms onderhevig aan andere beperkingen dan de interne logica van het netwerkschema. Deze worden weergegeven door opgedrongen datums.
Verdere verbeteringen, vooral voor de duidelijkheid bij de presentatie van de resultaten van kritieke pad analyse in een Gantt-chart, zijn het gebruik van mijlpalen en hammocks (hangmatten of groeperende activiteiten).
De beperkingen van kritieke pad analyse met betrekking tot het gebruik van één enkele schatting van de duur worden behandeld in technieken zoals PERT en Monte Carlo-analyse. De beperkingen met betrekking tot de beschikbaarheid van resources worden aangepakt in uitbreidingen op de techniek, zoals zwakste schakel en planning voor beperkte resources.
Met dank aan het BPUG-team voor de vertaling naar het Nederlands





