A análise do caminho crítico é uma técnica de programação de tempo para analisar um diagrama de rede. Ele calcula em qual data as atividades devem ocorrer no diagrama e identifica a flexibilidade na execução de algumas delas.
As duas importantes limitações da análise crítica do caminho são as seguintes:
- apenas uma duração estimada é usada para cada atividade;
- a técnica não faz concessões quanto à disponibilidade de recursos.
O cálculo compreende três fases:
- caminho de ida;
- caminho de volta;
- cálculos da folga.
O caminho de ida calcula o prazo mais cedo em que cada atividade pode ocorrer e o caminho de volta calcula o prazo mais tardio. A diferença entre os dois indica o grau de flexibilidade que existe no desempenho da atividade e isto é quantificado como folga.
Usando um computador, o modelo representado pelo diagrama de rede pode ser ajustado e estes cálculos podem ser realizados repetidas vezes. Isto permite que diferentes situações sejam testadas no que muitas vezes é chamado de análise de "e se" (what if).
Cada atividade no diagrama de redes terá sete elementos básicos:
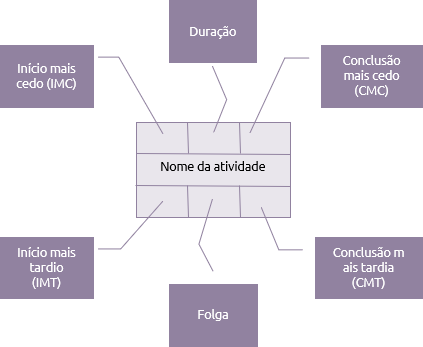
A duração é o tempo necessário para concluir a atividade. As datas superiores indicarão a data mais cedo que a atividade poderia ser realizada e as datas inferiores indicarão a data mais tardia que a atividade poderia ser realizada.
O caminho de ida:
O caminho de ida então começa colocando 0 como o primeiro início da atividade A. Como sua duração é de 2 dias, seu primeiro fim é o dia 2. Se A terminar no dia 2, então este é o início mais cedo para B e D, e assim se segue com os cálculos..
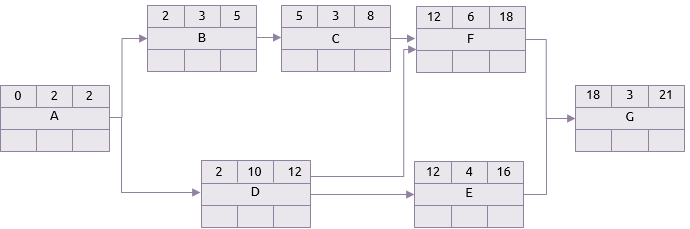
O próximo ponto a ser observado é a atividade F. Esta atividade tem dois predecessores C e D. O primeiro acabamento de C é 8, mas D é 12. Logo, o dia mais cedo de início de F é o dia 12.
Após o cálculo até sua conclusão, o primeiro final para G (e, portanto, o projeto) é de 21 dias.
O caminho de volta:
Presume-se que o encerramento mais cedo para o projeto seja também seu encerramento mais tardio. O processo é então repetido, mas ao contrário.
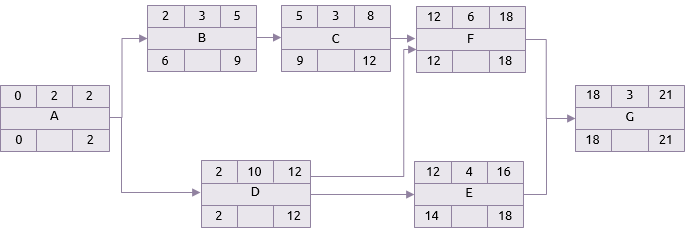
Se o último encerramento de G é 21, e a atividade leva 3 dias, seu último início é, portanto, o dia 18. Isso significa que F e E precisam terminar até o dia 18 no cenário mais tardio.
O início mais tardio de E é 14, de modo que D, talvez, tenha o término mais tardio em 14. Mas D também precisa ser concluída em tempo para F começar. O início mais tardio de F é dia 12, logo D precisa ter o término mais tardio 12 também..
O mesmo princípio se aplica a A. Mesmo que B não tenha que começar antes de 6, A deve ser terminado em 2 porque é a última data que D pode começar.
Cálculos de folga:
A última fase é a mais simples: Se houver diferença entre a data mais cedo e mais tardia que uma atividade pode ser concluída, ela precisa ter um grau de flexibilidade. Isto é calculado primeiro subtraindo o início mais cedo da conclusão mais tardia. O resultado é o tempo disponível para executar a atividade. Deduzindo o tempo necessário para executar a atividade (ou seja, a duração) do tempo disponível, calcula-se a folga total (ou "folga total").
Por exemplo, a atividade B::
Tempo disponível = conclusão mais tardia - início mais cedo (9-2)
Portanto, o tempo disponível é de 7 dias.
Folga total = tempo disponível - duração (7 - 3)
Portanto, a atividade B tem 4 dias de folga total, ou seja, poderia ser adiada ou prolongada por 4 dias sem estender a data de término da rede de 21 dias.
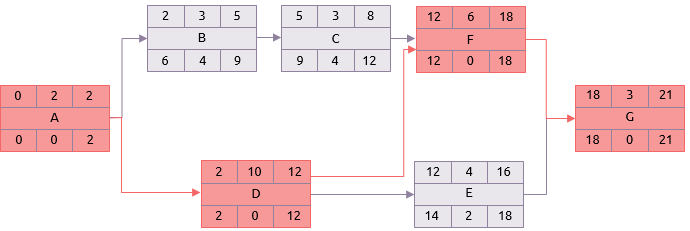
Para algumas atividades, o resultado deste cálculo será 0.
Por exemplo, a atividade D.
Folga = Conclusão mais tardia - Início mais cedo - duração (12-2-10)
Estas são as atividades críticas e a sequência destas desde a primeira até a última atividade é o caminho crítico. Para o diagrama exemplo, teríamos:
A-D-F-G.
O caminho crítico é o caminho mais longo através da rede e tem a menor folga (geralmente 0).
Neste exemplo simples há um único caminho crítico com flutuação zero, ou seja, há uma sequência de atividades sem nenhuma flexibilidade. Do ponto de vista gerencial, haverá inevitavelmente muitas atividades com pouca flexibilidade que também precisam de muita atenção quando se controla o projeto.
No exemplo, o foco será, A, D, F e G, porque eles não têm flexibilidade. Mas E tem apenas 2 dias de folga e também precisa ser vigiada cuidadosamente.
Há dois aspectos da folga que precisamos examinar mais de perto. Eles são demonstradas pelas atividades B e C.
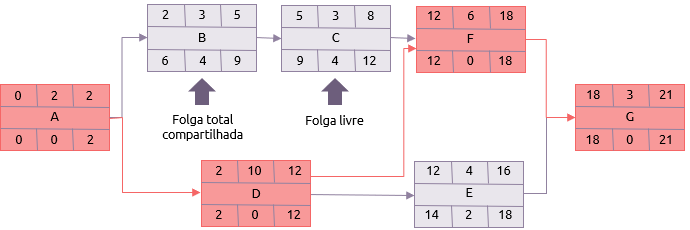
- Folga total compartilhada:
Se B for atrasada, terá efeito imediato sobre C. Isto é normalmente chamado apenas de folga total, embora seria mais preciso qualificá-lo como folga total "compartilhada".
- Folga livre:
Folga livre é o montante pelo qual uma atividade pode ser atrasada sem afetar nenhuma atividade subsequente. A atividade C pode ser adiada por até 4 dias sem ter efeito dominó, pois F não pode começar até o 12º dia de qualquer forma.
A rede do exemplo utiliza apenas as dependências concluir-para-iniciar. O uso de outros tipos de dependências de diagramas de rede torna o cálculo um pouco mais complexo e pode levar a atividades com diferentes quantidades de folga no início ou no fim. Isto é mais perceptível na análise de escadas.
As datas de início e conclusão das atividades às vezes estão sujeitas a outras restrições além da lógica interna do diagrama de rede. Estas são representadas por datas impostas.
Outras melhorias, principalmente para maior clareza ao apresentar os resultados da análise do caminho crítico em um gráfico Gantt, são o uso de marcos e varais.
As limitações da análise do caminho crítico em relação ao uso de uma única estimativa de duração são abordadas em técnicas como PERT e análise Monte Carlo. As limitações com relação à disponibilidade de recursos são abordadas em extensões da técnica, tais como cadeia crítica e programação limitada de recursos.





