Analisis jalur kritis adalah teknik penjadwalan waktu untuk menganalisis diagram jaringan. Dengan cara menghitung tanggal ketika kegiatan dalam jaringan harus terjadi dan mengidentifikasi fleksibilitas dalam kinerja beberapa kegiatan.
Dua batasan penting dari analisis jalur kritis adalah bahwa:
- hanya satu perkiraan durasi yang digunakan untuk setiap aktivitas;
- teknik ini tidak memberikan tunjangan untuk ketersediaan sumber daya.
Perhitungan terdiri dari tiga fase:
- hitungan maju;
- hitungan mundur;
- hitungan selisih.
Hitungan maju menghitung waktu paling awal ketika aktivitas dapat terjadi dan hitungan mundur menghitung waktu terakhir. Perbedaan antara keduanya menunjukkan tingkat fleksibilitas yang ada dalam kinerja aktivitas dan ini dikuantifikasi sebagai selisih.
Dengan menggunakan komputer, model yang diwakili oleh diagram jaringan, dapat disesuaikan dan perhitungan ini dapat dilakukan berulang kali lagi. Ini memungkinkan berbagai situasi berbeda untuk diuji dalam apa yang sering disebut analisis 'apa-jika'.
Setiap aktivitas dalam diagram jaringan akan memiliki tujuh elemen dasar:
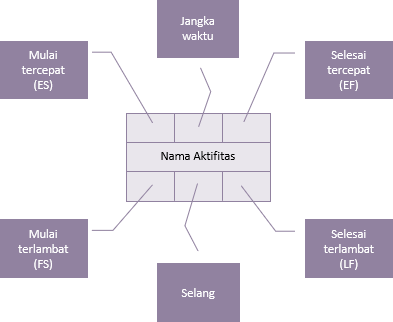
Durasi adalah waktu yang diperlukan untuk menyelesaikan aktivitas. Tanggal atas akan menunjukkan waktu paling awal kegiatan dapat dilakukan dan tanggal yang lebih rendah akan menunjukkan waktu terakhir kegiatan dapat dilakukan.
Hitungan Maju:
Hitungan maju kemudian dimulai dengan menempatkan 0 sebagai awal paling awal dari aktivitas A. Karena durasinya adalah 2 hari penyelesaian paling awal adalah hari 2. Jika A selesai pada hari ke 2 maka itu adalah awal dari B dan D, dan oleh karena itu perhitungan terus berlanjut.
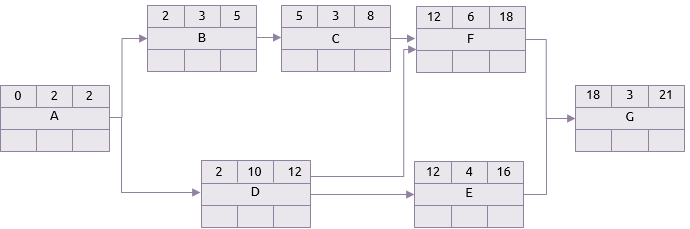
Hal berikutnya yang perlu diperhatikan adalah aktivitas F. Kegiatan ini memiliki dua pendahuluan C dan D. C yang paling awal selesai adalah 8 tetapi D adalah 12. Oleh karena itu waktu paling awal yang dapat dimulai F adalah hari ke-12.
Dengan mengikuti perhitungan ini hingga kesimpulannya, penyelesaian paling awal untuk G (dan karena itu proyek) adalah 21 hari.
Hitungan Mundur:
Penyelesaian paling awal untuk proyek ini diasumsikan juga merupakan penyelesaian terakhirnya. Proses ini kemudian diulang, tetapi sebaliknya.
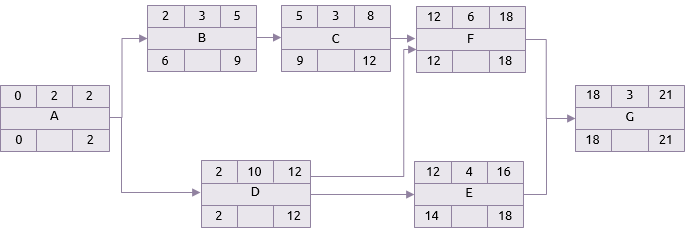
Jika selesai terakhir adalah hari ke-21, dan dibutuhkan waktu 3 hari, permulaan terakhirnya adalah hari ke-18. Ini berarti bahwa F dan E harus selesai paling lambat hari ke-18.
Awal paling baru adalah 14 dan karena itu, D, mungkin, memiliki penyelesaian terakhir 14. Tetapi D juga harus selesai tepat sebelum F dimulai. Awal terbaru dari F adalah 12 dan karenanya D memiliki akhir terbaru 12.
Prinsip yang sama berlaku untuk A. Meskipun B tidak harus dimulai hingga 6, A harus selesai oleh 2 karena ini adalah waktu terakhir D dapat dimulai.
Hitungan Selisih:
Fase terakhir adalah yang paling sederhana. Jika ada perbedaan antara waktu paling awal dan terkini yang dapat dilakukan suatu kegiatan, itu harus memiliki tingkat fleksibilitas. Ini dihitung dengan terlebih dahulu mulai dari awal paling akhir. Hasilnya adalah waktu yang tersedia untuk melakukan aktivitas. Dengan mengurangi waktu yang diperlukan untuk melakukan aktivitas (yaitu durasi) dari waktu yang tersedia, total selisih dihitung.
Misalnya, pada aktivitas B:
Waktu tersedia = selesai terbaru - awal paling awal (9 - 2)
Oleh karena itu waktu yang tersedia adalah 7 hari.
Total selisih = waktu yang tersedia - durasi (7 - 3)
Oleh karena itu aktivitas B memiliki 4 hari selisih total, yaitu dapat ditunda atau diperpanjang oleh 4 hari tanpa memperpanjang tanggal akhir jaringan 21 hari.
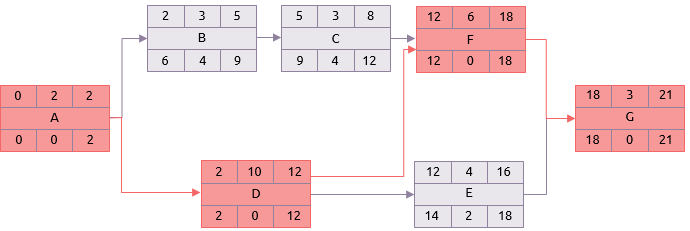
Pada beberapa aktivitas hasilnya akan menjadi 0.
Misalnya pada aktivitas D.
Selisih = Selesai terbaru - mulai paling awal - durasi (12-2-10)
Ini adalah kegiatan penting dan urutan ini dari kegiatan pertama hingga terakhir adalah jalur kritis. Di dalam jaringan contoh yaitu:
A-D-F-G.
Jalur kritis adalah jalur terpanjang melalui jaringan dan memiliki float paling sedikit (biasanya 0).
Dalam contoh sederhana ini ada satu jalur kritis dengan float nol yaitu ada urutan aktivitas tanpa fleksibilitas. Dari sudut pandang manajerial pasti akan ada banyak kegiatan dengan sejumlah kecil fleksibilitas yang juga perlu perhatian ketika mengendalikan proyek.
Dalam contoh fokusnya akan pada, A, D, F dan G, karena mereka tidak memiliki fleksibilitas. Tapi E hanya memiliki 2 hari selisih dan juga perlu diawasi dengan hati-hati.
Ada dua aspek selisih yang perlu kita perhatikan lebih dekat. Ini ditunjukkan oleh kegiatan B dan C.
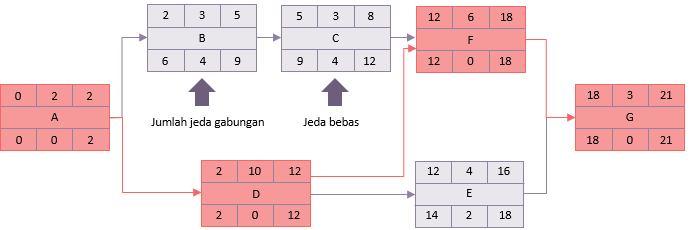
- Total selisih bersama
-
Jika B ditunda sama sekali, itu akan memiliki efek langsung pada C. Ini biasanya hanya disebut sebagai total selisih, meskipun akan lebih akurat untuk memenuhi syarat sebagai 'total' selisih.
- Selisih bebas
-
Selsih bebas adalah jumlah di mana suatu kegiatan dapat ditunda tanpa mempengaruhi kegiatan berikutnya. Aktivitas C dapat ditunda hingga 4 hari tanpa efek langsung karena F tidak dapat mulai sampai hari ke 12.
Jaringan contoh hanya menggunakan dependensi awal-ke-akhir. Penggunaan jenis lain dari ketergantungan diagram jaringan membuat perhitungan sedikit lebih rumit dan dapat menyebabkan aktivitas yang memiliki jumlah float yang berbeda pada awal atau akhir mereka. Ini paling terlihat dalam analisis tangga.
Tanggal mulai dan selesai kegiatan kadang-kadang tunduk pada kendala selain logika internal diagram jaringan. Ini diwakili oleh tanggal yang ditentukan.
Peningkatan lebih lanjut, terutama untuk kejelasan ketika menyajikan hasil analisis jalur kritis dalam bagan Gantt, adalah penggunaan tonggak dan gantungan.
Keterbatasan analisis jalur kritis sehubungan dengan penggunaan estimasi tunggal durasi dibahas dalam teknik seperti PERT dan analisis Monte Carlo. Keterbatasan yang berkaitan dengan ketersediaan sumber daya dibahas dalam ekstensi untuk teknik seperti rantai kritis dan penjadwalan sumber daya terbatas.
Terima kasih Valentinus Pramana untuk terjemahannya pada halaman ini.





