PERT é um acrônimo para "Program Evaluation and Review Technique" (Técnica de Revisão e Avaliação de Programa), desde a época em que o termo programa representava o cronograma de um projeto em vez de um programa de projetos e mudanças de negócio.
A análise do caminho crítico utiliza uma estimativa de um único ponto para todas as durações de atividade. Na realidade, é improvável que as durações possam ser estimadas com esse grau de certeza. A PERT usa uma estimativa de três pontos para cada atividade. As três estimativas são conhecidas como:
- Otimista (muito improvável que a tarefa demore menos do que isso);
- Pessimista (muito improvável que a tarefa demore mais que isso);
- Mais provável (duração que nós realmente pensamos que ocorrerá).
A tabela abaixo mostra sete atividades com durações otimista, mais provável e pessimista.
Tarefa | Otimista | Mais provável | Pessimista |
|---|---|---|---|
| A | 2 | 2 | 8 |
| B | 4 | 5 | 12 |
| C | 7 | 8 | 15 |
| D | 10 | 14 | 18 |
| E | 6 | 7 | 14 |
| F | 7 | 9 | 17 |
| G | 2 | 3 | 10 |
A utilização das durações mais prováveis em uma análise normal do caminho crítico dá o resultado mostrado abaixo, sendo o caminho crítico a seqüência: A, D, F, G.
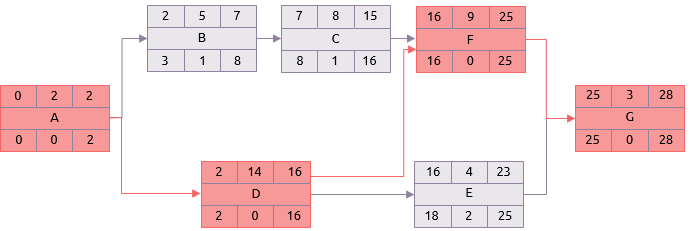
No entanto, as atividades vão usar algo entre as estimativas otimista e pessimista. A PERT utiliza estas estimativas para calcular uma duração média baseada em uma distribuição Beta.
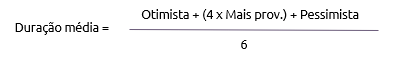
Ou para demonstrar formalmente:

Por exemplo, é mais provável que a atividade B demore 5 dias, mas há a possibilidade de que ela possa ser feita em 4 dias ou pode haver problemas que levem a até 12 dias.
Portanto, sua duração média é:

Uma tabela ampliada mostrando as durações médias para cada atividade é mostrada abaixo:
Tarefa | Otimista | Mais provável | Pessimista | Média |
|---|---|---|---|---|
| A | 2 | 2 | 8 | 3 |
| B | 4 | 5 | 12 | 6 |
| C | 7 | 8 | 15 | 9 |
| D | 10 | 14 | 18 | 14 |
| E | 6 | 7 | 14 | 8 |
| F | 7 | 9 | 17 | 10 |
| G | 2 | 3 | 10 | 4 |
A utilização das durações médias na análise em vez das estimativas mais prováveis dá um resultado diferente.
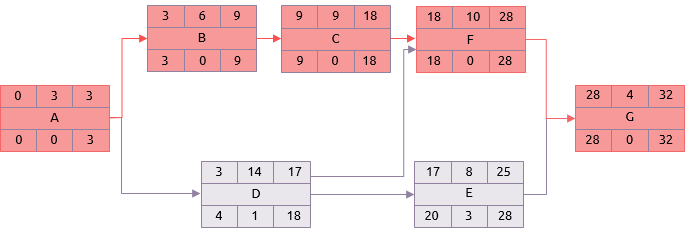
Não apenas a duração total do projeto aumentou para 32, mas o caminho crítico mudou. Agora compreende as tarefas A, B, C, F e G.
Mesmo que a PERT utilize três estimativas e, portanto, seja provável que dê um resultado mais realista, ela ainda fornece apenas um único resultado para a duração total do projeto. Este resultado está em uma distribuição normal e o desvio padrão (representado pela letra sigma) é usado para estimar a probabilidade de uma gama de datas de término do projeto.
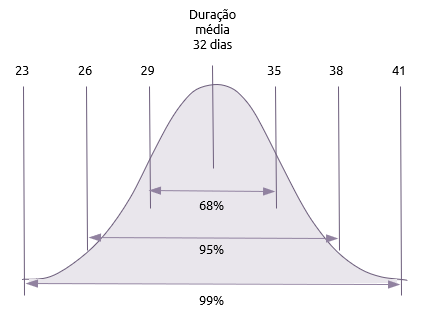
- 68% (Um-sigma)
-
Há uma chance de 68% (68,27 para ser mais preciso) de que o projeto leve entre mais ou menos um desvio padrão da média, ou seja, entre 32 - 3 (29 dias) e 32 + 3 (35 dias).
- 95% (Dois-sigmas)
-
Há uma chance de 95% (95,45 para ser mais preciso) de que o projeto leve entre mais ou menos dois desvios padrão da média, ou seja, entre 32-3-3 (26 dias) e 32+3+3 (38 dias).
- 99% (Três-sigmas)
-
Há uma chance de 99% (99,73 para ser mais preciso) de que serão necessários entre mais ou menos três desvios padrão da média, ou seja, entre 32-3-3-3 (23 dias) e 32+3+3+3+3 (41 dias).
O mesmo princípio pode ser usado para lidar com as faixas de custo estimadas em vez da duração do projeto. A PERT/Custo utiliza três estimativas do custo de cada atividade para calcular um custo médio para cada tarefa. O custo médio total do projeto é então a soma de todas as médias de custos das atividades, e não apenas aquelas no caminho crítico.
A PERT foi projetado quando a potência computacional estava a um preço especial. Este tipo de análise probabilística é agora normalmente realizada através da análise Monte Carlo.





