PERT est un acronyme pour « Program Evaluation and Review Technique » (technique d'évaluation et d'examen de programmes), à partir du moment où le programme à long terme représente l'échéancier d'un projet plutôt que d'un programme de projets et de changement.
L'analyse de chemin critique utilise une estimation de point unique pour toutes les durées d'activité. En réalité, il est peu probable que les durées puissent être estimées avec le degré de certitude. PERT utilise une estimation en trois points pour chaque activité. Les trois estimations sont connues comme :
- Optimiste (très peu probable que la tâche prenne moins longtemps que);
- Pessimiste (très peu probable que la tâche prenne plus longtemps que);
- Très probable (c’est ce que nous pensons vraiment qui arrivera).
Le tableau ci-dessous montre sept activités avec des durées optimistes, très probables et pessimistes.
Tâches | Optimiste | Plus probable | Pessimiste |
|---|---|---|---|
| A | 2 | 2 | 8 |
| B | 4 | 5 | 12 |
| C | 7 | 8 | 15 |
| D | 10 | 14 | 18 |
| E | 6 | 7 | 14 |
| F | 7 | 9 | 17 |
| G | 2 | 3 | 10 |
En utilisant les durées très probables, une analyse de chemin critique normale donne le résultat indiqué ci-dessous avec le chemin critique étant la séquence : A, D, F, G.
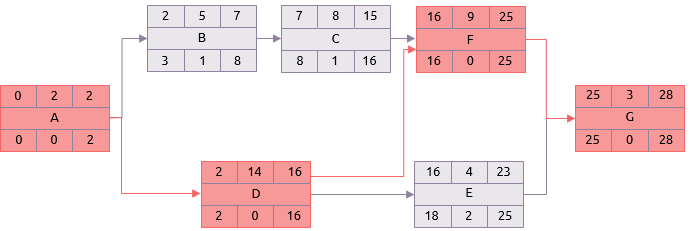
Cependant, les activités se situeront effectivement quelque part entre les estimations optimistes et pessimistes. PERT utilise ces estimations pour calculer une durée moyenne basée sur une distribution Beta.

Ou pour le montrer plus formellement :

Par exemple, l'activité B est le plus susceptible de prendre 5 jours, mais il y a une possibilité que cela puisse se faire en 4 jours ou il pourrait y avoir des problèmes, ce faisant pouvant prendre aussi longtemps que 12 jours.
Sa durée moyenne est donc :

Une table étendue montrant les durées moyennes pour chaque activité est représentée ci-dessous :
Tâche | Optimiste | Plus probable | Pessimiste | Moyenne |
|---|---|---|---|---|
| A | 2 | 2 | 8 | 3 |
| B | 4 | 5 | 12 | 6 |
| C | 7 | 8 | 15 | 9 |
| D | 10 | 14 | 18 | 14 |
| E | 6 | 7 | 14 | 8 |
| F | 7 | 9 | 17 | 10 |
| G | 2 | 3 | 10 | 4 |
En utilisant les durées moyennes dans l'analyse au lieu des estimations très probables, cela donne un résultat différent.
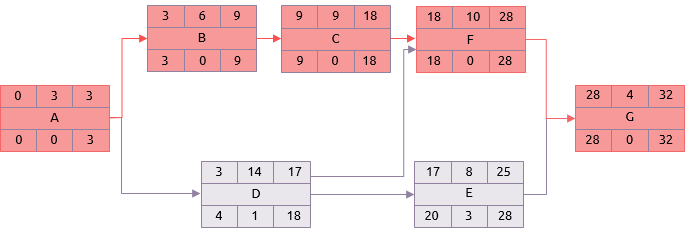
Non seulement la durée globale du projet a augmenté à 32, mais le chemin critique est déplacé. Il comprend désormais des tâches A, B, C, F et G.
Même si PERT utilise trois estimations, et donc est susceptible de donner un résultat plus réaliste, il fournit toujours un seul résultat pour la durée totale du projet. Ce résultat repose sur une distribution normale et l'écart-type (représenté par la lettre sigma) est utilisé pour estimer la probabilité d'une gamme de dates de fin de projet.
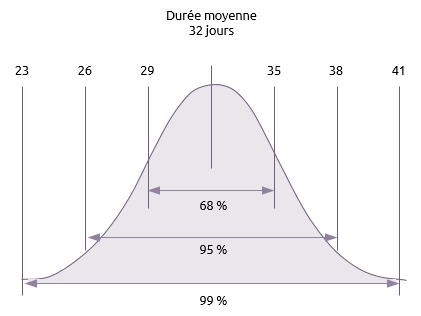
- 68 % [Un-sigma]
-
Il y a 68 % de chance [68,27 pour être précis] que le projet prenne entre plus ou moins un écart-type de la moyenne, à savoir entre 32 — 3 [29 jours] et 32 + 3 [35 jours].
- 95 % [Deux-sigma]
-
Il y a 95 % de chance [95,45 pour être précis] que le projet prenne entre plus ou moins deux écarts-types de la moyenne, à savoir entre 32-3-3 [26 jours] et 32 + 3 + 3 [38 jours].
- 99 % [Trois-sigma]
-
Il y a 99 % de chance [99,73 pour être précis] que cela prenne entre plus ou moins trois écarts-types de la moyenne, soit entre 32-3-3-3 [23 jours] et 32 + 3 + 3 + 3 [41 journées].
Plus précisément, le même principe peut être utilisé pour traiter des fourchettes estimées de coût plutôt que de la durée. PERT/Coût utilise trois estimations du coût de chaque activité pour calculer un coût moyen pour chaque tâche. Le coût total moyen du projet est alors la somme de toute l'activité moyenne et pas seulement ceux sur le chemin critique.
PERT a été conçue lorsque la puissance informatique était limitée. Ce type d'analyse probabiliste est maintenant normalement effectué en utilisant l’analyse Monte-Carlo.
Merci à la SMaP pour la traduction.





