PERT is een acroniem voor Program Evaluation and Review Technique. Vanaf het moment dat de term programma de planning van een project vertegenwoordigde in plaats van een programma van projecten en veranderingen in het bedrijf.
Bij de kritieke pad analyse wordt een 1-puntsschatting gebruikt voor alle activiteitsduren. In werkelijkheid is het onwaarschijnlijk dat de looptijden met een dergelijke mate van zekerheid kunnen worden ingeschat. PERT maakt voor elke activiteit gebruik van een 3-puntsschatting. De drie schattingen zijn bekend als:
- Optimistisch (zeer onwaarschijnlijk dat de taak korter zal duren dan dit);
- Pessimistisch (zeer onwaarschijnlijk dat de taak langer zal duren dan dit);
- Waarschijnlijk (dit is wat we echt denken dat het nodig zal zijn).
Onderstaande tabel geeft een overzicht van zeven activiteiten met optimistische, meest waarschijnlijke en pessimistische looptijden.
Taak | Optimistisch | Waarschijnlijk | Pessimistisch |
|---|---|---|---|
A | 2 | 2 | 8 |
B | 4 | 5 | 12 |
C | 7 | 8 | 15 |
D | 10 | 14 | 18 |
E | 6 | 7 | 14 |
F | 7 | 9 | 17 |
G | 2 | 3 | 10 |
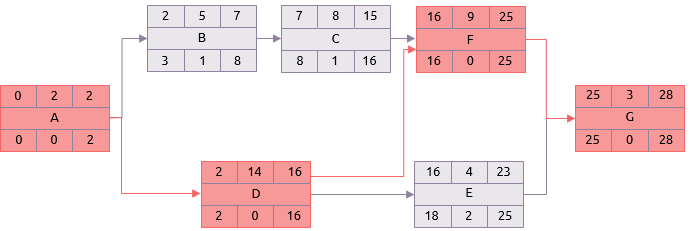
Het gebruik van de meest waarschijnlijke duur in een normale kritieke padanalyse geeft het hieronder getoonde resultaat, waarbij het kritieke pad de sequentie is: A, D, F, G.
Maar de activiteiten zullen eigenlijk ergens tussen de optimistische en de pessimistische inschattingen liggen. Op basis van deze schattingen berekent PERT een gemiddelde duur op basis van een bèta-distributie.

Of om het formeler te laten zien:

Activiteit B duurt bijvoorbeeld meestal 5 dagen, maar het is mogelijk dat dit in 4 dagen gebeurt of dat er problemen zijn waardoor het 12 dagen kan duren.
De gemiddelde duur ervan is dus:

Hieronder volgt een uitgebreide tabel met de gemiddelde duur per activiteit:
Taak | Optimistisch | Waarschijnlijk | Pessimistisch | Gemiddeld |
|---|---|---|---|---|
A | 2 | 2 | 8 | 3 |
B | 4 | 5 | 12 | 6 |
C | 7 | 8 | 15 | 9 |
D | 10 | 14 | 18 | 14 |
E | 6 | 7 | 14 | 8 |
F | 7 | 9 | 17 | 10 |
G | 2 | 3 | 10 | 4 |
Het gebruik van de gemiddelde duur in de analyse in plaats van de meest waarschijnlijke schattingen geeft een ander resultaat.
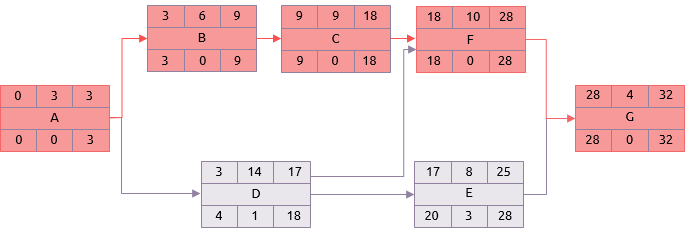
Niet alleen is de totale duur van het project toegenomen tot 32, maar ook is het kritieke pad bewogen. Het omvat nu de taken A, B, C, F en G.
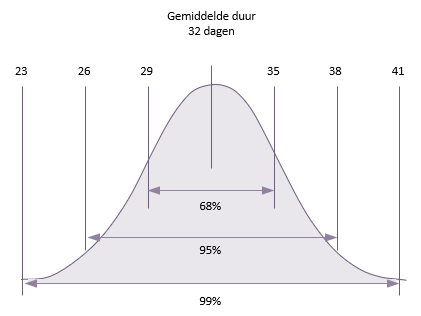
Hoewel PERT drie schattingen gebruikt en daardoor waarschijnlijk een realistischer resultaat zal geven, levert het slechts één resultaat op voor de totale duur van het project. Dit resultaat ligt op een normale verdeling en de standaarddeviatie (weergegeven door de letter sigma) wordt gebruikt om de waarschijnlijkheid van een reeks projecteinddata in te schatten.
- 68% (één-sigma)
-
De kans is 68% (68,27 om precies te zijn) dat het project één standaarddeviatie van het gemiddelde tussen de plus en min heeft, namelijk tussen de 32 - 3 (29 dagen) en 32 + 3 (35 dagen).
- 95% (tweesigma)
-
De kans is 95% (95,45 om precies te zijn) dat het project tussen plus of minus twee standaarddeviaties van het gemiddelde zal duren, namelijk tussen 32-3-3 (26 dagen) en 32+3+3 (38 dagen).
- 99% (drie-sigma)
-
De kans is 99% (99,37 om precies te zijn) dat het project tussen plus of minus 3 standaarddeviaties van het gemiddelde zal duren, namelijk tussen 32-3-3-3 (23 dagen) en 32+3+3+3 (41 dagen).
Precies hetzelfde beginsel kan worden gehanteerd voor de raming van de kostenmarges in plaats van voor de duur. PERT/Kosten gebruikt drie ramingen van de kosten van elke activiteit om de gemiddelde kosten voor elke taak te berekenen. De gemiddelde totale kosten van het project zijn dan de som van alle gemiddelde kosten van de activiteit en niet alleen die op het kritieke pad.
PERT is ontworpen toen rekenkracht nog in de kinderschoenen stond. Dit type probabilistische analyse wordt nu normaal uitgevoerd met Monte Carlo-analyse.
Met dank aan het BPUG-team voor de vertaling naar het Nederlands





