PERT è l’acronimo di Tecnica di Valutazione e di Revisione del Programma (Program Evaluation and Review Technique), dal momento in cui il termine ‘programma’ rappresenta la pianificazione di un progetto piuttosto che un programma di progetti e un cambiamento del business. L’analisi del cammino critico utilizza una valutazione basata su un’unica stima per tutte le durate delle attività. In realtà, è improbabile che le durate possano essere stimate con tale grado di certezza. PERT utilizza una valutazione a tre stime per ogni attività. Le tre stime sono note come:
- Ottimistica (molto improbabile che l’attività richieda una durata più breve di questa);
- Pessimistica (molto improbabile che l’attività richieda una durata maggiore di questa);
- Più probabile (questo è quanto realmente pensiamo che ci vorrà).
La tabella seguente mostra sette attività con le stime di durata ottimistiche, più probabili e pessimistiche.
Attivà | Durata ottimistica | Durata più probabile | Durata pessimistica |
|---|---|---|---|
| A | 2 | 2 | 8 |
| B | 4 | 5 | 12 |
| C | 7 | 8 | 15 |
| D | 10 | 14 | 18 |
| E | 6 | 7 | 14 |
| F | 7 | 9 | 17 |
| G | 2 | 3 | 10 |
L’utilizzo delle stime di durata più probabile in una normale analisi del cammino critico dà il risultato mostrato di seguito, con il percorso critico individuato dalla sequenza: A, D, F, G.
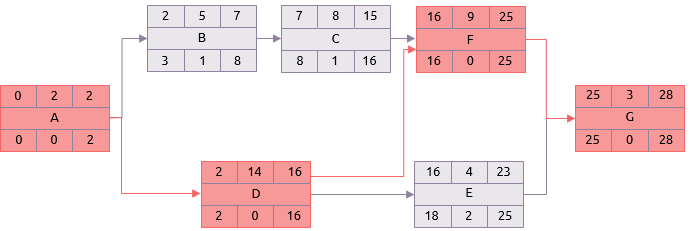
Tuttavia, le attività troveranno effettivamente la collocazione della loro durata da qualche parte tra le stime ottimistiche e pessimistiche. PERT utilizza queste stime per calcolare una durata media secondo una distribuzione Beta.

O per mostrarlo più formalmente:

Di seguito si riporta una tabella estesa che mostra le durate medie per ciascuna attività:
Attivà | Durata ottimistica | Durata più probabile | Durata pessimistica | Durata Media |
|---|---|---|---|---|
| A | 2 | 2 | 8 | 3 |
| B | 4 | 5 | 12 | 6 |
| C | 7 | 8 | 15 | 9 |
| D | 10 | 14 | 18 | 14 |
| E | 6 | 7 | 14 | 8 |
| F | 7 | 9 | 17 | 10 |
| G | 2 | 3 | 10 | 4 |
Utilizzando le durate medie nell’analisi invece delle stime più probabili si ottiene un risultato diverso.
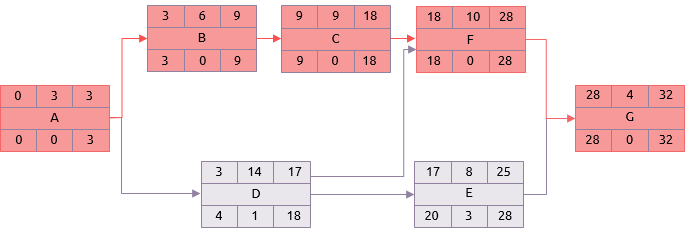
Non solo presenta la durata complessiva del progetto aumentata a 32, ma il cammino critico si è spostato. Esso comprende le attività A, B, C, F e G.
Anche se l’analisi PERT utilizza tre stime, ed è quindi probabile che dia un risultato più realistico, fornisce ancora un solo risultato per la durata complessiva del progetto. Questo risultato si trova su una distribuzione normale e la deviazione standard (rappresentata dalla lettera sigma) viene utilizzata per stimare la probabilità di un range di date di fine progetto.
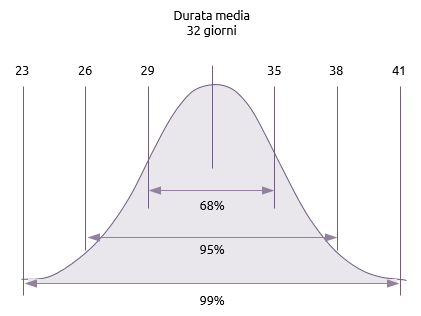
- 68% (Uno-sigma)
-
C’è una probabilità del 68% (68,27 per la precisione) che il progetto avrà tra più o meno una deviazione standard dalla media, cioè tra 32 – 3 (29 giorni), e 32 + 3 (35 giorni).
- 95% (Due-sigma)
-
C’è una probabilità del 95% (95,45 per la precisione) che il progetto avrà tra più o meno due deviazioni standard dalla media, cioè tra 32 – 3 – 3 (26 giorni), e 32 +3 + 3 (38 giorni).
- 99% (Tre-sigma)
-
C’è una probabilità del 99% (99,73 per la precisione) che l’attività assumerà una durata tra più o meno tre deviazioni standard dalla media, cioè tra 32 – 3 – 3 – 3 (23 giorni) e 32 +3 +3 +3 (41 giorni).
Esattamente lo stesso principio può essere applicato per trattare con intervalli stimati di costo, piuttosto che di durata. PERT/Cost utilizza tre stime del costo di ciascuna attività per calcolare un costo medio per ognuna di esse. Il costo medio totale del progetto è quindi la somma di tutti i costi medi delle attività, e non solo di quelle sul percorso critico.
PERT è stato concepito quando la potenza di calcolo era limitata. Questo tipo di analisi probabilistica è ora normalmente eseguito utilizzando l’analisi Monte Carlo.
Grazie ad E-quality Italia per la traduzione





